Bac 2021 (15 mars - sujet 1): Exponentielle et logarithme

Exercice corrigé - Spécialité maths, terminale générale

Soit 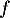$f$ la fonction définie sur l'intervalle $]0~;~ +\infty[$ par :
\[f(x) = \dfrac{e^x}x\]


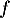On note $\mathcal{C}_f$ la courbe représentative de la fonction $f$ dans un repère orthonormé.


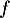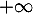    1. Préciser la limite de la fonction $f$ en $+ \infty$.
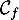    2. Justifier que l'axe des ordonnées est asymptote à la courbe $\mathcal{C}_f$.
  2. Montrer que, pour tout nombre réel 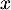$x$ de l'intervalle $]0~;~ +\infty[$, on a :
    \[f'(x)=\dfrac{e^x(x - 1)}{x^2}\]

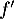    où $f'$ désigne la fonction dérivée de la fonction $f$.
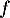  3. Déterminer les variations de la fonction 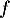$f$ sur l'intervalle $]0~;~ +\infty[$.
    On établira un tableau de variations de la fonction $f$ dans lequel apparaîtront les limites.
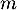  4. Soit $m$ un nombre réel. Préciser, en fonction des valeurs du nombre réel 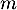$m$, le nombre de solutions de l'équation $f(x) = m$.
  5. On note $\Delta$ la droite d'équation $y = -x$.
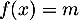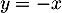    On note A un éventuel point de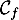 $\mathcal{C}_f$ d'abscisse 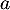$a$ en lequel la tangente à la courbe 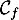$\mathcal{C}_f$ est parallèle à la droite $\Delta$.
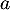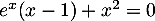    1. Montrer que $a$ est solution de l'équation $e^x(x-1) + x^2 = 0$.


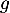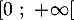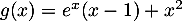      On note $g$ la fonction définie sur $[0~;~ +\infty[$ par $g(x)=e^x(x-1) + x^2 $.
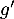      On admet que la fonction $g$ est dérivable et on note $g'$ sa fonction dérivée.
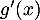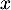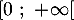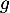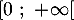    2. Calculer $g'(x)$ pour tout nombre réel $x$ de l'intervalle $[0~;~ +\infty[$, puis dresser le tableau de variations de $g$ sur $[0~;~+\infty[$.
    3. Montrer qu'il existe un unique point $A$ en lequel la tangente à 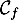$\mathcal{C}_f$ est parallèle à la droite $\Delta$.

Correction


Tags:LogarithmeExponentielle

Autres sujets au hasard: Lancer de dés

Voir aussi:

Quelques devoirs


LongPage: h2: 1 - h3: 0