Deux tangentes perpendiculaires

Exercice corrigé - Spécialité maths, terminale générale

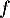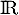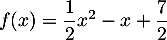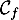Soit $f$ la fonction définie sur $\R$ par l'expression $f(x)=\dfrac12x^2-x+\dfrac72$ et $\mathcal{C}_f$ sa courbe représentative dans un repère orthonormal du plan.
Montrer que les tangentes à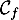 $\mathcal{C}_f$ aux points d'abscisse 0 et 2 sont perpendiculaires.

Correction
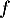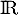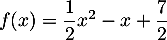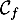Soit $f$ la fonction définie sur $\R$ par l'expression $f(x)=\dfrac12x^2-x+\dfrac72$ et $\mathcal{C}_f$ sa courbe représentative dans un repère orthonormal du plan.
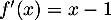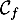On a $f'(x)=x-1$ et donc, la tangente à $\mathcal{C}_f$ en 0 a pour équation
\[\begin{array}{ll}T_0: &y=f'(0)(x-0)+f(0)=-x+\dfrac72\\[.4em] &\iff x+y-\dfrac72=0\enar\]

et la tangente à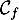 $\mathcal{C}_f$ en 2 a pour équation
\[\begin{array}{ll}T_2: &y=f'(2)(x-2)+f(2)=1(x-2)+\dfrac72=x+\dfrac32\\[.4em] &\iff -x+y-\dfrac32=0\enar\]

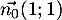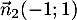Ainsi, $\vec{n_0}(1;1)$ et $\vec{n}_2(-1;1)$ sont des vecteurs normaux respectifs de ces deux droites, et comme
\[\vec{n}_0\cdot\vec{n}_2=1\tm(-1)+1\tm1=0\]

ces deux vecteurs sont orthogonaux, tout comme les droites qui sont donc bien perpendiculaires.

Cacher la correction


Tag:Fonctions

Autres sujets au hasard: Lancer de dés

Voir aussi:

Quelques devoirs


LongPage: h2: 1 - h3: 0