Deux équations avec logarithme

Exercice corrigé - Spécialité maths, terminale générale

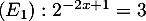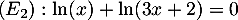
Résoudre les équations $(E_1): 2^{-2x+1}=3$ et $(E_2): \ln(x)+\ln(3x+2)=0$

Correction

\[\begin{array}{ll}&\hspace{-1em}(E_1):2^{-2x+1}=3\\[.5em] &\iff\ln\lp2^{-2x+1}\rp=\ln(3)\\[.5em] &\iff(-2x+1)\ln(2)=\ln(3)\\[.5em] &\iff(-2x+1)=\dfrac{\ln(3)}{\ln(2)}\\[.9em] &\iff x=-\dfrac12\lp\dfrac{\ln(3)}{\ln(2)}-1\right) \simeq-0,3 \enar\]

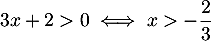Pour la deuxième équation, il faut que $x>0$ et que $3x+2>0\iff x>-\dfrac23$ soit donc, au final, on doit avoir $x>0$.
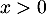Pour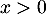 $x>0$, on a
\[\begin{array}{ll} &\hspace{-1em}(E_2):\ln(x)+\ln(3x+2)=0\\ &\iff\ln\bigl(x(3+2)\bigr)=0\\ &\iff x(3x+2)=e^0=1\\ &\iff 3x^2+2x-1=0\enar\]

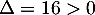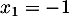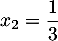Cette équation du second degré a pour discriminant $\Delta=16>0$ et admet deux racines $x_1=-1$ et $x_2=\dfrac13$.
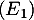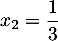La première racine n'est pas solution de l'équation $(E_1)$ qui a donc pour unique solution $x_2=\dfrac13$.

Cacher la correction


Tag:Logarithme

Autres sujets au hasard: Lancer de dés

Voir aussi:

Quelques devoirs


LongPage: h2: 1 - h3: 0