Bac 2022 (12 mai 2022): Trajectoire d'une balle de golf
Exercice corrigé - Spécialité maths, terminale générale
Partie A : études de deux fonctions
On considère les deux fonctions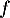 et
et 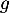 définies sur l'intervalle
définies sur l'intervalle 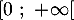 par:
par:
![\[f(x) = 0,06\left(-x^2 +13,7x\right)\quad \text{et}\quad g(x) = (-0,15x + 2,2)e^{0,2x} - 2,2.\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/4.png)
On admet que les fonctions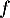 et
et 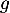 sont dérivables et on note
sont dérivables et on note 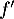 et
et 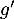 leurs fonctions dérivées respectives.
leurs fonctions dérivées respectives.
Partie B : trajectoires d'une balle de golf
Pour frapper la balle, un joueur de golf utilise un instrument appelé « club» de golf.
On souhaite exploiter les fonctions et
et 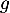 étudiées en Partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
étudiées en Partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
On admettra ici que est la valeur qui annule la fonction
est la valeur qui annule la fonction  et une approximation de la valeur qui annule la fonction
et une approximation de la valeur qui annule la fonction  .
.
On donne ci-dessous les représentations graphiques de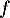 et
et 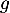 sur l'intervalle [0 ; 13,7].
sur l'intervalle [0 ; 13,7].
![$$(-1,-1)(14,3.5)
\psgrid[gridlabels=0pt,subgriddiv=1,gridwidth=0.2pt]
\psaxes[linewidth=1.25pt,Dx=20,Dy=20]{->}(0,0)(-1,-1)(14,3.5)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}\uput[ur](12,2.2){\blue $\mathcal{C}_g$}
\uput[dl](0,0){0}\uput[d](1,0){1}\uput[l](0,1){1}\uput[d](13.7,0){13,7}
$$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/34.png)
Pour représentant la distance horizontale parcourue par la balle en dizaine de yards après la frappe, (avec
représentant la distance horizontale parcourue par la balle en dizaine de yards après la frappe, (avec  ),
),  (ou
(ou 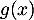 selon le modèle) représente la hauteur correspondante de la balle par rapport au sol, en dizaine de yards (1 yard correspond à environ
selon le modèle) représente la hauteur correspondante de la balle par rapport au sol, en dizaine de yards (1 yard correspond à environ 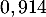 mètre).
mètre).
On appelle « angle de décollage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (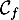 ou
ou 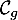 selon le modèle) en son point d'abscisse
selon le modèle) en son point d'abscisse  . Une mesure de l'angle de décollage de la balle est
un nombre réel
. Une mesure de l'angle de décollage de la balle est
un nombre réel 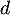 tel que
tel que 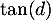 est égal au coefficient directeur de cette tangente.
est égal au coefficient directeur de cette tangente.
De même, on appelle « angle d'atterrissage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (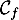 ou
ou 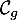 selon le modèle) en son point d'abscisse
selon le modèle) en son point d'abscisse  . Une mesure de l'angle d'atterrissage de la balle est un nombre réel
. Une mesure de l'angle d'atterrissage de la balle est un nombre réel 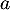 tel que
tel que 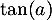 est égal à l'opposé du coefficient directeur de cette tangente.
est égal à l'opposé du coefficient directeur de cette tangente.
Tous les angles sont mesurés en degré.
(-0.3,-0.3)(14,3)
\psplot[plotpoints=1000]{0}{2}{0.822 x mul}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psline(13.7,0)(11,2)
\psarc(0,0){0.7}{0}{40}\rput(1.2,0.5){\footnotesize $d$}
\psarc(13.7,0){0.7}{140}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}&\psset{unit=0.5cm}
\begin{pspicture}(-0.3,-0.75)(14,3.5)
%\psgrid
\psaxes[linewidth=1.25pt,Dx=20,Dy=10](0,0)(-0.3,-0.5)(14,3)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}
\psline(0,0)(10.4,2.8)
\psline(13.7,0)(12,2.9)
\psarc(0,0){1}{0}{20}\rput(2,0.25){\footnotesize $d$}
\psarc(13.7,0){1}{120}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/50.png)
Partie C : interrogation des modèles
À partir d'un grand nombre d'observations des performances de joueurs professionnels, on a obtenu les résultats moyens suivants:
![\[\begin{tabular}{|*4{p{4.2cm}|}}\hline
Angle de d\'ecollage en degr\'e
&Hauteur maximale en yard
&Angle d'atterrissage en degr\'e
&Distance horizontale en yard au point de chute\\ \hline
24&32&52&137\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/61.png)
Quel modèle, parmi les deux étudiés précédemment, semble le plus adapté pour décrire la frappe de la balle par un joueur professionnel ? La réponse sera justifiée. Partie A : études de deux fonctions
On considère les deux fonctions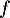 et
et 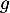 définies sur l'intervalle
définies sur l'intervalle  par:
par:
![\[f(x) = 0,06\left(-x^2 +13,7x\right)\quad \text{et}\quad g(x) = (-0,15x + 2,2)e^{0,2x} - 2,2.\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/65.png)
On admet que les fonctions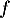 et
et 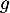 sont dérivables et on note
sont dérivables et on note  et
et 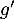 leurs fonctions dérivées respectives.
leurs fonctions dérivées respectives.
Partie B : trajectoires d'une balle de golf
Pour frapper la balle, un joueur de golf utilise un instrument appelé « club» de golf.
On souhaite exploiter les fonctions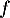 et
et  étudiées en Partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
étudiées en Partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
On admettra ici que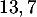 est la valeur qui annule la fonction
est la valeur qui annule la fonction 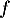 et une approximation de la valeur qui annule la fonction
et une approximation de la valeur qui annule la fonction 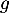 .
.
On donne ci-dessous les représentations graphiques de et
et 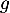 sur l'intervalle [0 ; 13,7].
sur l'intervalle [0 ; 13,7].
![$$(-1,-1)(14,3.5)
\psgrid[gridlabels=0pt,subgriddiv=1,gridwidth=0.2pt]
\psaxes[linewidth=1.25pt,Dx=20,Dy=20]{->}(0,0)(-1,-1)(14,3.5)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}\uput[ur](12,2.2){\blue $\mathcal{C}_g$}
\uput[dl](0,0){0}\uput[d](1,0){1}\uput[l](0,1){1}\uput[d](13.7,0){13,7}
$$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/95.png)
Pour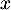 représentant la distance horizontale parcourue par la balle en dizaine de yards après la frappe, (avec
représentant la distance horizontale parcourue par la balle en dizaine de yards après la frappe, (avec  ),
),  (ou
(ou 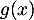 selon le modèle) représente la hauteur correspondante de la balle par rapport au sol, en dizaine de yards (1 yard correspond à environ
selon le modèle) représente la hauteur correspondante de la balle par rapport au sol, en dizaine de yards (1 yard correspond à environ 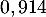 mètre).
mètre).
On appelle « angle de décollage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (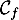 ou
ou  selon le modèle) en son point d'abscisse
selon le modèle) en son point d'abscisse  . Une mesure de l'angle de décollage de la balle est
un nombre réel
. Une mesure de l'angle de décollage de la balle est
un nombre réel 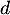 tel que
tel que 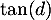 est égal au coefficient directeur de cette tangente.
est égal au coefficient directeur de cette tangente.
De même, on appelle « angle d'atterrissage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (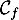 ou
ou 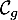 selon le modèle) en son point d'abscisse
selon le modèle) en son point d'abscisse 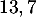 . Une mesure de l'angle d'atterrissage de la balle est un nombre réel
. Une mesure de l'angle d'atterrissage de la balle est un nombre réel 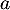 tel que
tel que  est égal à l'opposé du coefficient directeur de cette tangente.
est égal à l'opposé du coefficient directeur de cette tangente.
Tous les angles sont mesurés en degré.
(-0.3,-0.3)(14,3)
\psplot[plotpoints=1000]{0}{2}{0.822 x mul}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psline(13.7,0)(11,2)
\psarc(0,0){0.7}{0}{40}\rput(1.2,0.5){\footnotesize $d$}
\psarc(13.7,0){0.7}{140}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}&\psset{unit=0.5cm}
\begin{pspicture}(-0.3,-0.75)(14,3.5)
%\psgrid
\psaxes[linewidth=1.25pt,Dx=20,Dy=10](0,0)(-0.3,-0.5)(14,3)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}
\psline(0,0)(10.4,2.8)
\psline(13.7,0)(12,2.9)
\psarc(0,0){1}{0}{20}\rput(2,0.25){\footnotesize $d$}
\psarc(13.7,0){1}{120}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/111.png)
Partie C : interrogation des modèles
À partir d'un grand nombre d'observations des performances de joueurs professionnels, on a obtenu les résultats moyens suivants:
![\[\begin{tabular}{|*4{p{4.2cm}|}}\hline
Angle de d\'ecollage en degr\'e
&Hauteur maximale en yard
&Angle d'atterrissage en degr\'e
&Distance horizontale en yard au point de chute\\ \hline
24&32&52&137\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/122.png)
Quel modèle, parmi les deux étudiés précédemment, semble le plus adapté pour décrire la frappe de la balle par un joueur professionnel ? La réponse sera justifiée.
On considère les deux fonctions
On admet que les fonctions
- On donne le tableau de variations complet de la fonction
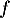 sur l'intervalle
sur l'intervalle 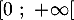 .
.
{$x$} \uput[u](1.6,1.4){$0$} \uput[u](4,1.4){$6,85$} \uput[u](6,1.4){$+ \infty$}
\rput(0.75,0.75){$f(x)$}\uput[u](1.65,0){$0$}\uput[d](4,1.5){$f(6,85)$}\uput[u](6,0){$- \infty$}
\psline{->}(1.9,0.4)(3.2,1.1)\psline{->}(4.8,1.1)(5.7,0.4)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/11.png)
- Justifier la limite de
 en
en  .
.
- Justifier les variations de la fonction
 .
.
- Résoudre l'équation
 .
.
- Justifier la limite de
-
- Déterminer la limite de
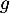 en
en 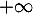 .
.
- Démontrer que, pour tout réel
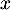 appartenant à
appartenant à 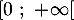 on a :
on a :  .
.
- Étudier les variations de la fonction
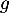 et dresser son tableau de variations sur
et dresser son tableau de variations sur 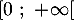 .
.
Préciser une valeur approchée à près du maximum de
près du maximum de 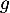 .
.
- Montrer que l'équation
 admet une unique solution non nulle et déterminer, à
admet une unique solution non nulle et déterminer, à  près, une valeur approchée de cette solution.
près, une valeur approchée de cette solution.
- Déterminer la limite de
Partie B : trajectoires d'une balle de golf
Pour frapper la balle, un joueur de golf utilise un instrument appelé « club» de golf.
On souhaite exploiter les fonctions
On admettra ici que
On donne ci-dessous les représentations graphiques de
![$$(-1,-1)(14,3.5)
\psgrid[gridlabels=0pt,subgriddiv=1,gridwidth=0.2pt]
\psaxes[linewidth=1.25pt,Dx=20,Dy=20]{->}(0,0)(-1,-1)(14,3.5)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}\uput[ur](12,2.2){\blue $\mathcal{C}_g$}
\uput[dl](0,0){0}\uput[d](1,0){1}\uput[l](0,1){1}\uput[d](13.7,0){13,7}
$$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/34.png)
Pour
On appelle « angle de décollage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (
De même, on appelle « angle d'atterrissage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (
Tous les angles sont mesurés en degré.
(-0.3,-0.3)(14,3)
\psplot[plotpoints=1000]{0}{2}{0.822 x mul}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psline(13.7,0)(11,2)
\psarc(0,0){0.7}{0}{40}\rput(1.2,0.5){\footnotesize $d$}
\psarc(13.7,0){0.7}{140}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}&\psset{unit=0.5cm}
\begin{pspicture}(-0.3,-0.75)(14,3.5)
%\psgrid
\psaxes[linewidth=1.25pt,Dx=20,Dy=10](0,0)(-0.3,-0.5)(14,3)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}
\psline(0,0)(10.4,2.8)
\psline(13.7,0)(12,2.9)
\psarc(0,0){1}{0}{20}\rput(2,0.25){\footnotesize $d$}
\psarc(13.7,0){1}{120}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/50.png)
- Première modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et 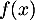 la hauteur correspondante de la balle.
la hauteur correspondante de la balle.
Selon ce modèle :- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
- Vérifier que
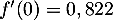 .
.
- Donner une mesure en degré de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
- Quelle propriété graphique de la courbe
 permet de justifier que les angles de décollage et d'atterrissage de la balle sont égaux ?
permet de justifier que les angles de décollage et d'atterrissage de la balle sont égaux ?
- Seconde modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et  la hauteur correspondante de la balle.
Selon ce modèle :
la hauteur correspondante de la balle.
Selon ce modèle :
- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
On précise que
 et
et 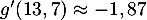 .
.
- Donner une mesure en degré de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
- Justifier que
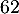 est une valeur approchée, arrondie à l'unité près, d'une mesure en degré de l'angle d'atterrissage de la balle.
est une valeur approchée, arrondie à l'unité près, d'une mesure en degré de l'angle d'atterrissage de la balle.
Tableau : extrait d'une feuille de calcul donnant une mesure en degré d'un angle quand on connait sa tangente :
![\[%\begin{tabularx}{\linewidth}{|c|*{13}{>{\centering \arraybackslash}X|}}
\begin{tabular}{|c|p{2em}|*{12}{c|}}
\hline
&A&B&C&D&E&F&G&H&I&J&K&L&M\\ \hline
1&$\!\!\tan(\theta)$&0,815&0,816&0,817&0,818&0,819&0,82&0,821&0,822&0,823&0,824&0,825&0,826\\ \hline
2&\scriptsize \mbox{$\theta$ en} degr\'es&39,18&39,21&39,25&39,28&39,32&39,35&39,39&39,42&39,45&39,49&39,52&39,56\\ \hline
3& &&&&&&&&&&&&\\ \hline
4&$\!\!\tan(\theta)$&0,285& 0,286& 0,287& 0,288& 0,289&0,29&0,291&0,292&
0,293&0,294&0,295 &0,296\\ \hline
5&\scriptsize \mbox{$\theta$ en} degr\'es&15,91 &15,96&16,01& 16,07& 16,12& 16,17& 16,23& 16,28& 16,33& 16,38& 16,44& 16,49\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/60.png)
- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
On précise que
Partie C : interrogation des modèles
À partir d'un grand nombre d'observations des performances de joueurs professionnels, on a obtenu les résultats moyens suivants:
![\[\begin{tabular}{|*4{p{4.2cm}|}}\hline
Angle de d\'ecollage en degr\'e
&Hauteur maximale en yard
&Angle d'atterrissage en degr\'e
&Distance horizontale en yard au point de chute\\ \hline
24&32&52&137\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/61.png)
Quel modèle, parmi les deux étudiés précédemment, semble le plus adapté pour décrire la frappe de la balle par un joueur professionnel ? La réponse sera justifiée. Partie A : études de deux fonctions
On considère les deux fonctions
On admet que les fonctions
- On donne le tableau de variations complet de la fonction
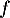 sur l'intervalle
sur l'intervalle 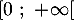 .
.
{$x$} \uput[u](1.6,1.4){$0$} \uput[u](4,1.4){$6,85$} \uput[u](6,1.4){$+ \infty$}
\rput(0.75,0.75){$f(x)$}\uput[u](1.65,0){$0$}\uput[d](4,1.5){$f(6,85)$}\uput[u](6,0){$- \infty$}
\psline{->}(1.9,0.4)(3.2,1.1)\psline{->}(4.8,1.1)(5.7,0.4)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/72.png)
- Justifier la limite de
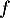 en
en  .
.
- Justifier les variations de la fonction
 .
.
- Résoudre l'équation
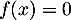 .
.
- Justifier la limite de
-
- Déterminer la limite de
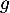 en
en  .
.
- Démontrer que, pour tout réel
 appartenant à
appartenant à  on a :
on a :  .
.
- Étudier les variations de la fonction
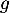 et dresser son tableau de variations sur
et dresser son tableau de variations sur 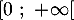 .
.
Préciser une valeur approchée à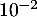 près du maximum de
près du maximum de  .
.
- Montrer que l'équation
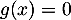 admet une unique solution non nulle et déterminer, à
admet une unique solution non nulle et déterminer, à  près, une valeur approchée de cette solution.
près, une valeur approchée de cette solution.
- Déterminer la limite de
Partie B : trajectoires d'une balle de golf
Pour frapper la balle, un joueur de golf utilise un instrument appelé « club» de golf.
On souhaite exploiter les fonctions
On admettra ici que
On donne ci-dessous les représentations graphiques de
![$$(-1,-1)(14,3.5)
\psgrid[gridlabels=0pt,subgriddiv=1,gridwidth=0.2pt]
\psaxes[linewidth=1.25pt,Dx=20,Dy=20]{->}(0,0)(-1,-1)(14,3.5)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}\uput[ur](12,2.2){\blue $\mathcal{C}_g$}
\uput[dl](0,0){0}\uput[d](1,0){1}\uput[l](0,1){1}\uput[d](13.7,0){13,7}
$$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/95.png)
Pour
On appelle « angle de décollage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (
De même, on appelle « angle d'atterrissage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (
Tous les angles sont mesurés en degré.
(-0.3,-0.3)(14,3)
\psplot[plotpoints=1000]{0}{2}{0.822 x mul}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psline(13.7,0)(11,2)
\psarc(0,0){0.7}{0}{40}\rput(1.2,0.5){\footnotesize $d$}
\psarc(13.7,0){0.7}{140}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}&\psset{unit=0.5cm}
\begin{pspicture}(-0.3,-0.75)(14,3.5)
%\psgrid
\psaxes[linewidth=1.25pt,Dx=20,Dy=10](0,0)(-0.3,-0.5)(14,3)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}
\psline(0,0)(10.4,2.8)
\psline(13.7,0)(12,2.9)
\psarc(0,0){1}{0}{20}\rput(2,0.25){\footnotesize $d$}
\psarc(13.7,0){1}{120}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/111.png)
- Première modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et  la hauteur correspondante de la balle.
la hauteur correspondante de la balle.
Selon ce modèle :- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
- Vérifier que
 .
.
- Donner une mesure en degré de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
- Quelle propriété graphique de la courbe
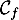 permet de justifier que les angles de décollage et d'atterrissage de la balle sont égaux ?
permet de justifier que les angles de décollage et d'atterrissage de la balle sont égaux ?
- Seconde modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
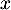 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et 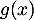 la hauteur correspondante de la balle.
Selon ce modèle :
la hauteur correspondante de la balle.
Selon ce modèle :
- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
On précise que
 et
et 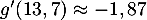 .
.
- Donner une mesure en degré de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
- Justifier que
 est une valeur approchée, arrondie à l'unité près, d'une mesure en degré de l'angle d'atterrissage de la balle.
est une valeur approchée, arrondie à l'unité près, d'une mesure en degré de l'angle d'atterrissage de la balle.
Tableau : extrait d'une feuille de calcul donnant une mesure en degré d'un angle quand on connait sa tangente :
![\[%\begin{tabularx}{\linewidth}{|c|*{13}{>{\centering \arraybackslash}X|}}
\begin{tabular}{|c|p{2em}|*{12}{c|}}
\hline
&A&B&C&D&E&F&G&H&I&J&K&L&M\\ \hline
1&$\!\!\tan(\theta)$&0,815&0,816&0,817&0,818&0,819&0,82&0,821&0,822&0,823&0,824&0,825&0,826\\ \hline
2&\scriptsize \mbox{$\theta$ en} degr\'es&39,18&39,21&39,25&39,28&39,32&39,35&39,39&39,42&39,45&39,49&39,52&39,56\\ \hline
3& &&&&&&&&&&&&\\ \hline
4&$\!\!\tan(\theta)$&0,285& 0,286& 0,287& 0,288& 0,289&0,29&0,291&0,292&
0,293&0,294&0,295 &0,296\\ \hline
5&\scriptsize \mbox{$\theta$ en} degr\'es&15,91 &15,96&16,01& 16,07& 16,12& 16,17& 16,23& 16,28& 16,33& 16,38& 16,44& 16,49\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/121.png)
- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
On précise que
Partie C : interrogation des modèles
À partir d'un grand nombre d'observations des performances de joueurs professionnels, on a obtenu les résultats moyens suivants:
![\[\begin{tabular}{|*4{p{4.2cm}|}}\hline
Angle de d\'ecollage en degr\'e
&Hauteur maximale en yard
&Angle d'atterrissage en degr\'e
&Distance horizontale en yard au point de chute\\ \hline
24&32&52&137\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/122.png)
Quel modèle, parmi les deux étudiés précédemment, semble le plus adapté pour décrire la frappe de la balle par un joueur professionnel ? La réponse sera justifiée.
Correction
Partie A : études de deux fonctions
Partie B : trajectoires d'une balle de golf
Partie C : interrogation des modèles
Les angles de décollage et d'atterissage sont très clairement différents, et le modèle parabolique de la fonction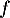 n'est donc clairement pas adapté.
n'est donc clairement pas adapté.
La hauteur maximale est aussi mieux approchée par le second modèle.
Parmi les deux modèles étudiés, le modèle fourni par la fonction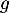 semble donc
le plus adapté.
semble donc
le plus adapté.
Cacher la correction
Partie A : études de deux fonctions
-
- On a, pour tout
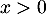 ,
,
![\[f(x)=-0,06x^2\lp1-\dfrac{13,7}x\rp\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/2.png)
avec
![\[\lim_{x\to+\infty}-0,06x^2=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/3.png)
et
![\[\lim_{x\to+\infty}\lp1-\dfrac{13,7}x\rp=1\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/4.png)
d'où, par produit, la limite
![\[\lim_{x\to+\infty}f(x)=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/5.png)
- On a
 d'où le tableau de signes et de variations
d'où le tableau de signes et de variations
![\[\begin{tabular}{|c|*5c|}\hline
$x$ & 0 && 6,85 && $+\infty$ \\\hline
$-2x+13,7$&& $+$ &\zb&$-$&\\\hline
$f'(x)$&& $+$ &\zb&$-$&\\\hline
&&&$f(6,85)$&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/7.png)
- On a
![\[\begin{array}{ll}f(x) = 0&\iff -x^2+13,7x=0\\
&\iff x(-x+13,7)=0\\
&\iff x=0 \text{ ou } x=13,7\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/8.png)
- On a, pour tout
-
- On a
![\[\lim_{x\to+\infty}(-0,15x+2,2)=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/9.png)
et
![\[\lim_{x\to+\infty}e^{0,2x}=+\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/10.png)
et donc, par produit,
![\[\lim_{x\to+\infty}(-0,15x+2,2)e^{0,2x}=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/11.png)
et donc aussi,
![\[\lim_{x\to+\infty}g(x)=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/12.png)
- On a
 avec
avec
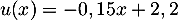 et
et  et
et 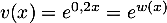 donc
donc
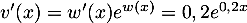 .
.
On obtient donc , soit pour tout
, soit pour tout  ,
,
![\[\begin{array}{ll}g'(x)&=-0,15e^{0,2x}+(-0,15x+2,2)\tm0,2e^{0,2x}\\
&=\Bigl(-0,15+0,2(-0,15x+2,2)\Bigr)e^{0,2x}\\
&=\lp-0,03x+0,29\right) e^{0,2x}
\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/20.png)
- On obtient alors le tableau de signes et de variations:
![\[\begin{tabular}{|c|*5c|}\hline
$x$ & 0 && $29/3$ && $+\infty$ \\\hline
$-0,03x+0,29$&& $+$ &\zb&$-$&\\\hline
$e^{0,2x}$&& $+$ &\vline&$+$&\\\hline
$g'(x)$&& $+$ &\zb&$-$&\\\hline
&&&$g\lp29/3\rp$&&\\
$g$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&0&&&&$-\infty$\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/21.png)
On trouve comme valeur maximale
![\[g\lp\dfrac{29}3\rp\simeq2,98\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/22.png)
- on a pour tout
![$x\in]0;29/3]$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/23.png) ,
, 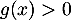 et donc l'équation
et donc l'équation 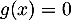 n'admet aucune soltuion.
n'admet aucune soltuion.
Sur , la fonction
, la fonction 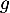 est continue (car même dérivable),
strictement décroissante
avec
est continue (car même dérivable),
strictement décroissante
avec  et
et
 .
.
Ainsi, d'après le théorème des valeurs intermédiaires, ou théorème de la bijection, l'équation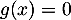 admet une unique solution sur
admet une unique solution sur 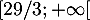 .
.
Finalement, l'équation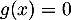 admet une unique solution sur
admet une unique solution sur ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/33.png) , c'est-à-dire une unique solution non nulle.
, c'est-à-dire une unique solution non nulle.
Avec la calculatrice, par balayage ou dichotomie par exemple, on trouve comme valeur approchée de cette solution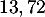 .
.
- On a
Partie B : trajectoires d'une balle de golf
- Première modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et 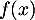 la hauteur correspondante de la balle.
la hauteur correspondante de la balle.
Selon ce modèle :- On a vu que le maximum de
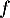 est
est 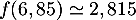 soit une hauteur maximale de 28,15 yards.
soit une hauteur maximale de 28,15 yards.
- On a
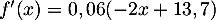 ,
d'où
,
d'où  .
.
-
 est le coefficient directeur de la tangente à la courbe de
est le coefficient directeur de la tangente à la courbe de 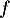 en 0,
c'est-à-dire justement au décollage.
en 0,
c'est-à-dire justement au décollage.
On a donc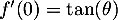 et donc, d'après le tableau donné dans
l'énoncé,
et donc, d'après le tableau donné dans
l'énoncé, 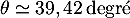 .
.
- La courbe est une parabole. En particulier, elle est symétrique par rapport à la droite
 , abscisse de son sommet.
Les points de décollage
, abscisse de son sommet.
Les points de décollage 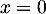 et d'atterissage
et d'atterissage 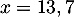 sont symétriques eux aussi par rapport à cette droite, et il en est donc de même des angles
que forment les tangentes à la courbes en ces deux points,
c'est-à-dire que les angles de décollage et d'atterrissage de la balle sont
égaux.
sont symétriques eux aussi par rapport à cette droite, et il en est donc de même des angles
que forment les tangentes à la courbes en ces deux points,
c'est-à-dire que les angles de décollage et d'atterrissage de la balle sont
égaux.
- On a vu que le maximum de
- Seconde modélisation
- D'après ce modèle, la hauteur maximale est
![\[g\lp\dfrac{29}3\rp\simeq2,98\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/48.png)
soit 29,8 yard. On précise que et .
.
-
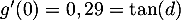 soit, d'après le tableau foruni,
soit, d'après le tableau foruni, 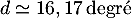 .
.
- De même pour l'angle d'atterissage,
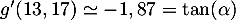 soit
soit 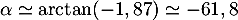 soit,
arrondie à l'unité près, environ 62 degrés.
soit,
arrondie à l'unité près, environ 62 degrés.
- D'après ce modèle, la hauteur maximale est
Partie C : interrogation des modèles
Les angles de décollage et d'atterissage sont très clairement différents, et le modèle parabolique de la fonction
La hauteur maximale est aussi mieux approchée par le second modèle.
Parmi les deux modèles étudiés, le modèle fourni par la fonction
Cacher la correction
Tag:Exponentielle
Voir aussi:
