Bac 2022 (11 mai): Un peu de tout dans l'espace
Exercice corrigé - Spécialité maths, terminale générale
Dans l'espace rapporté à un repère orthonormé 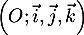 ,
on considère:
,
on considère:
- le point A de coordonnées
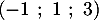 ,
, - la droite
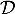 dont une représentation paramétrique est:
dont une représentation paramétrique est:
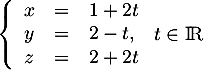 .
.
-
- Donner les coordonnées d'un vecteur directeur
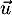 de la droite
de la droite 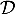 .
On admet que le point A n'appartient pas à la droite
.
On admet que le point A n'appartient pas à la droite 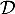 .
.
- Montrer que le point
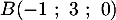 appartient à la droite
appartient à la droite 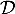 .
.
- Calculer le produit scalaire
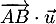 .
.
- Donner les coordonnées d'un vecteur directeur
- On note
 le plan passant par le point A et orthogonal à la droite
le plan passant par le point A et orthogonal à la droite 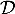 , et on appelle H le point d'intersection du plan
, et on appelle H le point d'intersection du plan 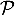 et de la droite
et de la droite 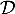 . Ainsi, H est le projeté orthogonal de A sur la droite
. Ainsi, H est le projeté orthogonal de A sur la droite 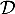 .
.
- Montrer que le plan
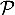 admet pour équation cartésienne:
admet pour équation cartésienne: 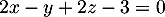 .
.
- En déduire que le point H a pour coordonnées
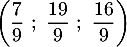 .
.
- Calculer la longueur AH. On donnera une valeur exacte.
- Montrer que le plan
- Dans cette question, on se propose de retrouver les coordonnées du point H, projeté orthogonal du point A sur la droite
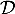 , par une autre méthode.
On rappelle que le point B
, par une autre méthode.
On rappelle que le point B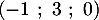 appartient à la droite
appartient à la droite 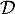 et que le vecteur
et que le vecteur 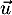 est un vecteur directeur de la droite
est un vecteur directeur de la droite 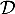 .
.
- Justifier qu'il existe un nombre réel
 tel que
tel que 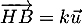 .
.
- Montrer que
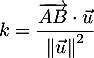 .
.
- Calculer la valeur du nombre réel
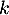 et retrouver les coordonnées du point H.
et retrouver les coordonnées du point H.
- Justifier qu'il existe un nombre réel
- On considère un point C appartenant au plan
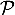 tel que le volume du tétraèdre ABCH soit égal à
tel que le volume du tétraèdre ABCH soit égal à  .
Calculer l'aire du triangle ACH.
.
Calculer l'aire du triangle ACH.
On rappelle que le volume d'un tétraèdre est donné par: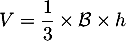 où
où  désigne l'aire d'une base
et
désigne l'aire d'une base
et 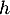 la hauteur relative à cette base.
la hauteur relative à cette base.
Correction
Cacher la correction
-
- Un vecteur directeur est donné par
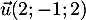
- Avec les coordonnées de B, on a
![\[\la\begin{array}{lcl}
-1&=&1+2t\\3 &=& 2 - t,\\0&=& 2+2t
\enar\right.
\iff
\la\begin{array}{lcl}
t&=&-1\\t&=&-1,\\t&=&-1
\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/2.png)
ce qui montre que B appartient bien à la droite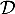 .
.
- On a
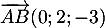 donc
donc
![\[\overrightarrow{AB}\cdot\vec{u}=0\tm2+2\tm(-1)+(-3)\tm2=-8\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/5.png)
- Un vecteur directeur est donné par
-
(4,0)
\psline(4,0)(4,-2)
\rput(4,1){$\tm$}\rput(4.3,1.2){$H$}
\rput(3.7,3.5){$\mathcal{D}$}
\psline[linecolor=blue,linewidth=2pt]{->}(4,-1.5)(4,-.5)
\psline[linecolor=blue](3.92,-1.5)(4.08,-1.5)
\rput(4.25,-1.1){\blue$\vec{u}$}
\rput(4,2.6){$\tm$}\rput(4.3,2.7){$B$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/6.png)
- Le plan
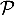 est orthogonale à la droite
est orthogonale à la droite 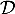 dirigée par
dirigée par
 qui est donc un vecteur normal à ce plan qui admet
donc une équation cartésienne de la forme
qui est donc un vecteur normal à ce plan qui admet
donc une équation cartésienne de la forme
![\[2x-y+2z+d=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/10.png)
On sait de plus que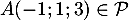 , et donc que
, et donc que
![\[2(-1)-(1)+2(3)+d=0\iff d=-3\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/12.png)
Finalement, on a trouvé une équation cartésienne du plan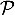 :
:
![\[\mathcal{P}: 2x - y + 2z - 3 = 0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/14.png)
- Le plan
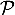 et la droite
et la droite 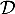 sont orthogonaux;
en particulier ils se coupent en un unique point
sont orthogonaux;
en particulier ils se coupent en un unique point 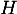 .
.
Soit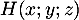 , alors
, alors
![\[H\in\mathcal{D}\iff
\la\begin{array}{lcl}
x&=&1+2t\\y &=& 2 - t,\\z&=& 2+2t
\enar\right. t \in \R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/19.png)
et de plus,
![\[\begin{array}{ll}H\in\mathcal{P}&\iff 2x - y + 2z - 3 = 0\\
&\iff2(1+2t)-(2-t)+2(2+2t)-3=0\\
&\iff t=-\dfrac19
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/20.png)
et on obtient alors les coordonnées
![\[\la\begin{array}{lcl}
x&=&1+2\tm\lp-1\frac19\rp=\frac79\\[.4em]
y &=& 2 - \lp-\frac19\rp=\frac{19}9\\[.4em]
z&=& 2+2\lp-\frac19\rp=\frac{16}9
\enar\right. t \in \R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/21.png)
qui sont bien les coordonnées recherchées du point H.
-
![\[\begin{array}{ll}
AH&=\sqrt{\lp\dfrac79-(-1)\rp^2+\lp\dfrac{19}9-1\rp^2+\lp\dfrac{16}9-3\rp^2}\\
&=\sqrt{\dfrac{16^2+10^2+11^2}{9^2}}
=\dfrac{\sqrt{253}}9
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/22.png)
- Le plan
-
- Les points H et B appartiennent tous les deux à la droite
 ,
et
,
et  est un vecteur directeur de cette droite.
est un vecteur directeur de cette droite.
On en déduit que les vecteurs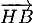 et
et 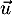 sont colinéaires,
c'est-à-dire qu'il existe un réel
sont colinéaires,
c'est-à-dire qu'il existe un réel 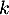 tel que
tel que
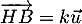 .
.
- D'après le résultat précédent, en prenant le produit scalaire
avec
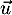 on obtient
on obtient
![\[\overrightarrow{HB}=k\vec{u}\implies \overrightarrow{HB}\cdot\vec{u}=k\vec{u}\cdot\vec{u}=\left\|\vec{u}\right\|^2\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/30.png)
d'où
![\[k=\dfrac{\overrightarrow{HB}\cdot\vec{u}}{\left\|\vec{u}\right\|^2}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/31.png)
Maintenant pour faire intervenir le vecteur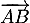 on peut utiliser la
relation de Chasles:
on peut utiliser la
relation de Chasles:
![\[\overrightarrow{HB}=\overrightarrow{HA}+\overrightarrow{AB}
\implies
\overrightarrow{HB}\cdot\vec{n}=\overrightarrow{HA}\cdot\vec{n}+\overrightarrow{AB}\cdot\vec{n}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/33.png)
or car
car 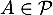 et
et 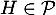 et
et 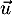 normal à
normal à 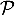 .
.
On vient donc de trouver que
![\[\overrightarrow{HB}\cdot\vec{n}=\overrightarrow{AB}\cdot\vec{n}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/39.png)
et donc la relation souhaitée:
![\[k=\dfrac{\overrightarrow{HB}\cdot\vec{u}}{\left\|\vec{u}\right\|^2}
=\dfrac{\overrightarrow{AB}\cdot\vec{u}}{\left\|\vec{u}\right\|^2}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/40.png)
-
D'après la question 1.c. on a
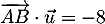 ,
et comme
,
et comme 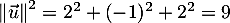 , on obtient
que
, on obtient
que
![\[k=\dfrac{-8}9\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/43.png)
et on retrouve les coordonnées du point H(x;y;z):
![\[\overrightarrow{HB}=k\vec{u}
\iff
\la\begin{array}{lcl}
-1-x&=&-\dfrac89\tm2\\
3-y&=&-\dfrac89\tm(-1)\\
0-z&=&-\dfrac89\tm2
\enar\right.
\iff
\la\begin{array}{lcl}
x&=&-1+\dfrac{16}9=\dfrac79\\
y&=&3-\dfrac89=\dfrac{19}9\\
z&=&\dfrac{16}9
\enar\right.
\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/44.png)
- Les points H et B appartiennent tous les deux à la droite
- BH est une hauteur relative à la base ACH,
et donc, avec
![\[V = \dfrac13 \times \mathcal{B} \times h\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/45.png)
avec
![\[\begin{array}{ll}
h&=BH=\sqrt{\lp\dfrac79-(-1)\rp^2+\lp\dfrac{19}9-3\rp^2+\lp\dfrac{16}9-0\rp^2}\\
&=\sqrt{\dfrac{16^2+8^2+16^2}{9^2}}
=\dfrac{8}{9}\sqrt{9}=\dfrac{24}9
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/46.png)
et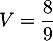 ,
d'où l'aire de la base ACH:
,
d'où l'aire de la base ACH:
![\[\dfrac89=\dfrac13\tm\mathcal{B}\tm\dfrac{24}{9}
\iff
\mathcal{B}=1\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/48.png)
Cacher la correction
Tag:Géométrie dans l'espace
Voir aussi:
