Bac 2021 (Sujet 0): Un peu de tout dans l'espace, dans un cube
Exercice corrigé - Spécialité maths, terminale générale
|
On considère le cube Dans tous les exercices, l'espace est rapporté au repère orthonormé |

\psline(4,0.5)(4,3.5)
\psline(4,3.5)(1,3.5)
\psline(0,3)(1,3.5)
\psline(3,3)(4,3.5)
\psline[linestyle=dashed](1,0.5)(4,0.5)
\psline[linestyle=dashed](3,0)(4,.5)
\psline[linestyle=dashed](1,0.5)(1,3.5)
\rput(-0.2,-0.2){$A$}
\rput(3.2,-0.2){$B$}
\rput(4.3,0.6){$C$}
\rput(1.2,0.7){$D$}
\rput(-.2,3){$E$}
\rput(2.95,3.2){$F$}
\rput(4.3,3.7){$G$}
\rput(.7,3.7){$H$}
\rput(1.5,2.98){$\tm$}\rput(1.5,2.65){$I$}
\psline[linewidth=.5pt](3,3)(6,3)
\rput(6,2.98){$\tm$}\rput(5.9,2.65){$J$}
$$](/Generateur-Devoirs/TS/ChapGeomSpace/ex0/8.png) |
-
- Par lecture graphique, donner les coordonnées de
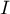 et
et 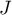 .
.
- En déduire les coordonnées des vecteurs
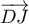 ,
, 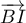 et
et  .
.
- Montrer que
 est un vecteur normal au plan
est un vecteur normal au plan  .
.
- Montrer qu'une équation cartésienne du plan
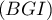 est
est
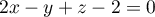 .
.
- Par lecture graphique, donner les coordonnées de
- On note
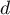 la droite passant par
la droite passant par 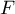 et orthogonale au plan
et orthogonale au plan  .
.
- Déterminer une représentation paramétrique de la droite
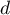 .
.
- On considère le point
 de coordonnées
de coordonnées
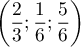 .
.
Montrer que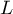 est le point d'intersection de la droite
est le point d'intersection de la droite 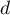 et du plan
et du plan 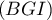 .
.
- Déterminer une représentation paramétrique de la droite
- On rappelle que le volume
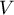 d'une pyramide est donné par la formule
d'une pyramide est donné par la formule
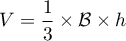 ,
où
,
où  est l'aire d'une base et
est l'aire d'une base et 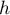 la hauteur associée à cette base.
la hauteur associée à cette base.
- Calculer le volume de la pyramide
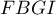 .
.
- En déduire l'aire du triangle
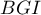 .
.
- Calculer le volume de la pyramide
Correction
Cacher la correction

\psline(4,0.5)(4,3.5)
\psline(4,3.5)(1,3.5)
\psline(0,3)(1,3.5)
\psline(3,3)(4,3.5)
\psline[linestyle=dashed](1,0.5)(4,0.5)
\psline[linestyle=dashed](3,0)(4,.5)
\psline[linestyle=dashed](1,0.5)(1,3.5)
\rput(-0.2,-0.2){$A$}
\rput(3.2,-0.2){$B$}
\rput(4.3,0.6){$C$}
\rput(1.2,0.7){$D$}
\rput(-.2,3){$E$}
\rput(2.95,3.2){$F$}
\rput(4.3,3.7){$G$}
\rput(.7,3.7){$H$}
\rput(1.5,2.98){$\tm$}\rput(1.5,2.65){$I$}
\psline[linewidth=.5pt](3,3)(6,3)
\rput(6,2.98){$\tm$}\rput(5.9,2.65){$J$}
$$](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/1.png) |
-
- Par lecture graphique,
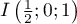 et
et 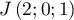 .
.
- On en déduit
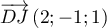 ,
,
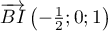 et
et
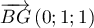 .
.
-
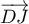 est normal au plan
est normal au plan 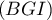 si et seulement si il est orthogonal à deux vecteurs non colinéaires du plan, par exemple
si et seulement si il est orthogonal à deux vecteurs non colinéaires du plan, par exemple
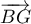 et
et 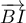 , ce qui est bien le cas car:
, ce qui est bien le cas car:
![\[\overrightarrow{DJ}\cdot\overrightarrow{BG}=2\tm0+(-1)\tm1+1\tm1=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/11.png)
et
![\[\overrightarrow{DJ}\cdot\overrightarrow{BI}=2\tm\lp-\dfrac12\rp+(-1)\tm0+1\tm1=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/12.png)
- Un vecteur normal au plan
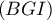 est donc
est donc 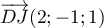 et donc ce plan a une équation cartésienne de la forme
et donc ce plan a une équation cartésienne de la forme
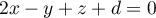 .
.
De plus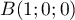 appartient à ce plan, d'où
appartient à ce plan, d'où
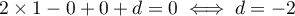 .
.
Une équation cartésienne du plan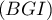 est donc bien
est donc bien
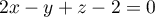 .
.
- Par lecture graphique,
- On note
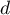 la droite passant par
la droite passant par 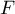 et orthogonale au plan
et orthogonale au plan 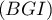 .
.
- Comme la droite
 est orthogonale au plan
est orthogonale au plan 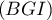 et que
et que 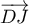 est aussi orthogonal à ce plan, on en déduit que
est aussi orthogonal à ce plan, on en déduit que 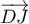 est un vecteur directeur de
est un vecteur directeur de 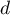 . On a donc une reprsentation paramétrique, avec
. On a donc une reprsentation paramétrique, avec 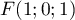 :
:
![\[d:\la\begin{array}{ccr}
x&=&1+2t\\
y&=&-t\\
z&=&1+t\enar\right.
\ , t \in\R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/29.png)
- Comme
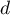 est orthogonal à
est orthogonal à 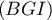 , leur intersection est donc un point. Il reste donc simplement à vérifier que cette intersection est le point
, leur intersection est donc un point. Il reste donc simplement à vérifier que cette intersection est le point 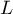 , c'est-à-dire que
, c'est-à-dire que 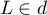 et
et 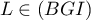 .
.
Avec l'équation cartésienne de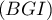 ,
,
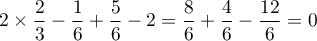 et donc
et donc 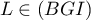 .
.
Avec la représentation prarémtrique de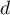 , on cherche
, on cherche 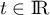 tel que
tel que
![\[d:\la\begin{array}{ccl}
\frac23&=&1+2t\\[.4em]
\frac16&=&-t\\[.4em]
\frac56&=&1+t\enar\right.
\iff t=-\dfrac16\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/40.png)
et donc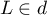 .
.
Finalement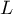 est le point d'intersection de
est le point d'intersection de 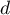 et
et 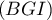 .
.
- Comme la droite
-
- D'après tout ce qui précède, une hauteur est
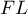 associée à la base
associée à la base 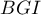 .
.
On peut aussi considérer la base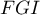 associée à la hauteur
associée à la hauteur 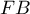 , qui donne
le volume
, qui donne
le volume
![\[\begin{array}{ll}V&=\dfrac13\tm\lp\dfrac12 FI\tm FG\rp\tm FB\\[1em]
&=\dfrac13\tm\lp\dfrac12\tm\dfrac12\tm1\rp\tm1
=\dfrac1{12}
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/49.png)
- En utilisant la hauteur
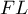 et la base
et la base 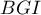 d'aire
d'aire 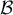 ,
on a
,
on a
![\[V=\dfrac13\tm\mathcal{B}\tm FL\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/53.png)
où
![\[FL=\sqrt{\lp\dfrac23-1\rp^2+\lp\dfrac16-0\rp^2+\lp\dfrac56-1\rp^2}
=\sqrt{\dfrac16}
=\dfrac1{\sqrt6}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/54.png)
On en déduit que
![\[V=\dfrac1{12}=\dfrac13\tm\mathcal{B}\tm\dfrac1{\sqrt6}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/55.png)
d'où l'aire du triangle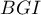 .
.
![\[\mathcal{B}=\dfrac{\sqrt6}4\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/57.png)
- D'après tout ce qui précède, une hauteur est
Cacher la correction
Tag:Géométrie dans l'espace
Voir aussi:
