Oral de Bac - Position relative de droites dans l'espace, représentations paramétriques
Exercice corrigé - Spécialité maths, terminale générale
Dans l'espace muni du repère orthonormal 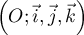 on considère les droites
on considère les droites 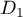 ,
, 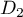 et
et 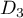 de représentations paramétriques:
de représentations paramétriques:
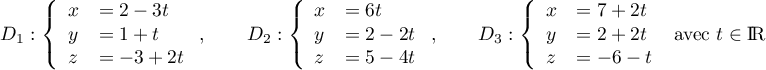
Etudier la position relative des droites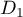 et
et 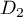 , puis
, puis 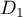 et
et 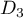 ,
et enfin
,
et enfin 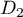 et
et 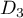 .
.
Correction
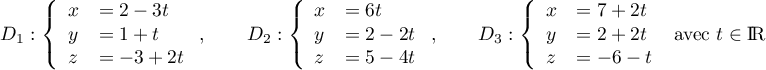
Etudier la position relative des droites
Correction
Tag:Géométrie dans l'espace
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie plane analytique, vecteurs et équations de droites, géométrie avec une hyperbole et ses tangentes, courbe représentative de la fonction inverse
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle - Analyse: étude d'une fonction: variations, limites, TVI, asymptotes, ...
étude de la convexité de fonctions (et variations, tangentes, limites, ...) et géométrie dans l'espace
