Bac 2021 (Amérique du nord): Géométrie dans un cube
Exercice corrigé - Spécialité maths, terminale générale
On considère un cube ABCDEFGH. Le point I est le milieu du segment [EF], le point J est le milieu du segment [BC] et le point K est le milieu du segment [AE].
{A} \uput[dr](5.5,0){B} \uput[u](5.5,5){F} \uput[ul](0.5,5.4){E}
\psline(5.5,0)(8.5,1.4)(8.5,6.4)(5.5,5)%BCGF
\uput[r](8.5,1.4){C} \uput[ur](8.5,6.4){G}
\psline(8.5,6.4)(3.5,6.8)(0.5,5.4)%GHE
\uput[u](3.5,6.8){H} \uput[u](3,5.2){I}\uput[dr](7,0.7){J}\uput[l](0.5,2.9){K}
\psline[linewidth=1.6pt](0.5,0.4)(3,5.2)%AI
\psline[linestyle=dashed,linewidth=1.6pt](3,5.2)(7,0.7)%IJ
\psline[linestyle=dashed,linewidth=1.6pt](0.5,2.9)(3.5,6.8)%KH
\psline[linestyle=dashed](0.5,0.4)(3.5,1.8)(3.5,6.8)%ADH
\uput[ur](3.5,1.8){D}
\psline[linestyle=dashed](3.5,1.8)(8.5,1.4)%DC
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21/1.png)
{A} \uput[dr](5.5,0){B} \uput[u](5.5,5){F} \uput[ul](0.5,5.4){E}
\psline(5.5,0)(8.5,1.4)(8.5,6.4)(5.5,5)%BCGF
\uput[r](8.5,1.4){C} \uput[ur](8.5,6.4){G}
\psline(8.5,6.4)(3.5,6.8)(0.5,5.4)%GHE
\uput[u](3.5,6.8){H} \uput[u](3,5.2){I}\uput[dr](7,0.7){J}\uput[l](0.5,2.9){K}
\psline[linewidth=1.6pt](0.5,0.4)(3,5.2)%AI
\psline[linestyle=dashed,linewidth=1.6pt](3,5.2)(7,0.7)%IJ
\psline[linestyle=dashed,linewidth=1.6pt](0.5,2.9)(3.5,6.8)%KH
\psline[linestyle=dashed](0.5,0.4)(3.5,1.8)(3.5,6.8)%ADH
\uput[ur](3.5,1.8){D}
\psline[linestyle=dashed](3.5,1.8)(8.5,1.4)%DC
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21/1.png)
-
Les droites (AI) et (KH) sont-elles parallèles ? Justifier votre réponse,
Dans la suite, on se place dans le repère orthonormé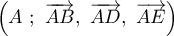 .
.
-
- Donner les coordonnées des points I et J.
- Montrer que les vecteurs
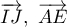 et
et 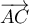 sont coplanaires.
sont coplanaires.
On considère le plan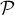 d'équation
d'équation 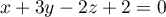 ainsi que les droites
ainsi que les droites 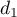 et
et 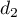 définies par les représentations
paramétriques ci-dessous:
définies par les représentations
paramétriques ci-dessous:
![\[d_1 : \left\{\begin{array}{l c l}
x &=&3 + t\\
y &=& 8 - 2t\\
z &=& - 2 + 3t\\
\end{array}\right. , t \in \R\quad \text{et}\quad
d_2 : \left\{\begin{array}{l c l}
x &=&4 + t\\
y &=&1 + t\\
z &=&8 + 2t\\
\end{array}\right. , t \in \R.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21/9.png)
- Les droites
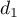 et
et 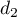 sont-elles parallèles ? Justifier votre réponse.
sont-elles parallèles ? Justifier votre réponse.
- Montrer que la droite
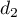 est parallèle au plan
est parallèle au plan 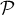 .
.
- Montrer que le point L(4 ; 0 ; 3) est le projeté orthogonal du point M(5 ; 3 ; 1) sur le plan
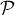 .
.
Correction
Baccalauréat général, spécialité mathématique, Amérique du Nord mai 2021 (candidats libres)
{A} \uput[dr](5.5,0){B} \uput[u](5.5,5){F} \uput[ul](0.5,5.4){E}
\psline(5.5,0)(8.5,1.4)(8.5,6.4)(5.5,5)%BCGF
\uput[r](8.5,1.4){C} \uput[ur](8.5,6.4){G}
\psline(8.5,6.4)(3.5,6.8)(0.5,5.4)%GHE
\uput[u](3.5,6.8){H} \uput[u](3,5.2){I}\uput[dr](7,0.7){J}\uput[l](0.5,2.9){K}
\psline[linewidth=1.6pt](0.5,0.4)(3,5.2)%AI
\psline[linestyle=dashed,linewidth=1.6pt](3,5.2)(7,0.7)%IJ
\psline[linestyle=dashed,linewidth=1.6pt](0.5,2.9)(3.5,6.8)%KH
\psline[linestyle=dashed](0.5,0.4)(3.5,1.8)(3.5,6.8)%ADH
\uput[ur](3.5,1.8){D}
\psline[linestyle=dashed](3.5,1.8)(8.5,1.4)%DC
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/1.png)
Cacher la correction
Baccalauréat général, spécialité mathématique, Amérique du Nord mai 2021 (candidats libres)
{A} \uput[dr](5.5,0){B} \uput[u](5.5,5){F} \uput[ul](0.5,5.4){E}
\psline(5.5,0)(8.5,1.4)(8.5,6.4)(5.5,5)%BCGF
\uput[r](8.5,1.4){C} \uput[ur](8.5,6.4){G}
\psline(8.5,6.4)(3.5,6.8)(0.5,5.4)%GHE
\uput[u](3.5,6.8){H} \uput[u](3,5.2){I}\uput[dr](7,0.7){J}\uput[l](0.5,2.9){K}
\psline[linewidth=1.6pt](0.5,0.4)(3,5.2)%AI
\psline[linestyle=dashed,linewidth=1.6pt](3,5.2)(7,0.7)%IJ
\psline[linestyle=dashed,linewidth=1.6pt](0.5,2.9)(3.5,6.8)%KH
\psline[linestyle=dashed](0.5,0.4)(3.5,1.8)(3.5,6.8)%ADH
\uput[ur](3.5,1.8){D}
\psline[linestyle=dashed](3.5,1.8)(8.5,1.4)%DC
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/1.png)
- On a A(0;0;0) et I(0,5;0;1), donc
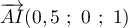 et K(0;0;0,5) et H(0;1;1)
donc
et K(0;0;0,5) et H(0;1;1)
donc 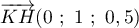 .
.
Ces vecteurs ne sont pas colinéaires, donc les droites (AI) et (KH) ne sont pas parallèles.
-
- On a par lecture graphique I(0,5;0;1), et J(1;0,5;0)
- On a
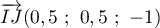 ,
, 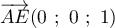 , et
, et
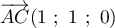 .
.
On a donc que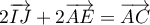 ,
ce qui montre que ces trois vecteurs sont coplanaires.
,
ce qui montre que ces trois vecteurs sont coplanaires.
Autre méthode 2, si on ne s'aperçoit pas de la relation suivante, on peut tous simplement la chercher: on cherche s'il existe trois réels a,b et c tels que
![\[a\overrightarrow{IJ}+b\overrightarrow{AE}+c\overrightarrow{AC}=\vec{0}
\iff\la\begin{array}{rcrcrcl}
0,5a&+& &+&c &=&0\\
0,5a&+& &+&c &=&0\\
-a&+& b&& &=&0\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/8.png)
dont la troisième équation donne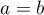 puis
puis 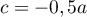 , et il y a une infinité de solutions, par
exemple
, et il y a une infinité de solutions, par
exemple 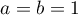 et
et 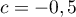 ,
d'où la relation
,
d'où la relation
![\[\overrightarrow{IJ}+\overrightarrow{AE}-0,5\overrightarrow{AC}=\vec{0}
\iff \overrightarrow{IJ}=-\overrightarrow{AE}+0,5\overrightarrow{AC}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/13.png)
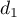 a pour vecteur directeur
a pour vecteur directeur 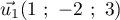 et
et 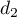 a pour vecteur directeur
a pour vecteur directeur 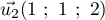 : ces vecteurs ne sont pas colinéaires, donc les droites
: ces vecteurs ne sont pas colinéaires, donc les droites 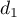 et
et 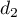 ne sont pas parallèles
ne sont pas parallèles
- Un vecteur directeur de
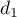 est
est 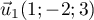 et un vecteur directeur de
et un vecteur directeur de 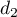 est
est 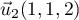 .
.
Ces deux vecteurs ne sont pas colinéaires donc les droites ne sont pas parallèles.
- Le plan a pour vecteur normal le vecteur
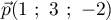 et
et 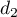 a pour vecteur directeur
a pour vecteur directeur 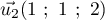 .
.
Or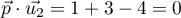 :
les vecteurs sont orthogonaux donc la droite
:
les vecteurs sont orthogonaux donc la droite 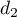 est parallèle
au plan
est parallèle
au plan 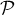 .
.
-
Méthode 1. Soit
 la perpendiculaire à
la perpendiculaire à 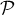 contenant M. Cette droite a pour vecteur directeur le vecteur
contenant M. Cette droite a pour vecteur directeur le vecteur 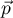 , donc une équation paramétrique de
, donc une équation paramétrique de  est :
est :
![\[\la\begin{array}{rcl}
x&=&5 + 1t\\
y&=&3 + 3t\\
z&=&1 - 2t\\
\enar\right., t \in \R.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/34.png)
Le projeté L, de M sur le plan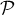 a ses coordonnées qui vérifient les quatre équations:
a ses coordonnées qui vérifient les quatre équations:
![\[\left\{\begin{array}{rcl}
x&=&5 + 1t\\
y&=&3 + 3t\\
z&=&1 - 2t\\
x + 3y - 2z + 2&=&0
\end{array}\right. , t \in \R.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/36.png)
et donc, en substituant les expressions des coordonnées dans la dernière équation du plan, on obtient
![\[5 + t + 3(3 + 3t) - 2(1 - 2t) + 2 = 0
\iff t = - 1\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/37.png)
En reportant dans les trois premières équations du système, on trouve alors les coordonnées de L projeté orthogonal de M sur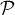 :
:
![\[\la\begin{array}{lcl}
x&=&5 - 1\\
y&=&3 + 3\times (- 1)\\
z&=&1 - 2\times (- 1)\\
\enar\right. \iff
\la\begin{array}{l c l}
x&=&4\\
y&=&0\\
z&=&3\\
\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/39.png)
Donc le projeté orthogonal de M sur le plan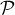 est le le point L(4 ; 0 ; 3).
est le le point L(4 ; 0 ; 3).
Méthode 2. On a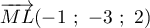 ,
donc
,
donc 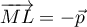 est un vecteur normal au plan
est un vecteur normal au plan 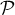 .
.
D'autre part
![\[L(4~;~0~;~3)\in\mathcal{P}\iff 4 + 3 \times 0 - 2 \times 3 + 2 = 6 - 6 = 0\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/44.png)
est vraie, donc L est bien le projeté orthogonal de M sur le plan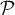 .
.
Cacher la correction
Tag:Géométrie dans l'espace
Voir aussi:
