Bac 2021 (15 mars 2021): exponentielles, distance entre deux courbes
Exercice corrigé - Spécialité maths, terminale générale
Le graphique suivant représente, dans un repère orthogonal, les courbes
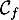 et
et 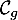 des fonctions
des fonctions  et
et  définies sur
définies sur  par:
par:
![\[f(x) = x^2e^{-x}\quad \text{ et } \quad g(x) = e^{-x}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/6.png)
(2.5,\n)}
\multido{\n=-2+1}{5}{\psline[linewidth=0.1pt,linestyle=dashed](\n,-1)(\n,9)}
\psaxes[linewidth=1.25pt,labelFontSize=\scriptstyle,Dy=2]{->}(0,0)(-2.5,-1)(2.5,9)
\psplot[linewidth=1.5pt,linecolor=blue,plotpoints=2000]{-2.5}{2.5}{x dup mul 2.71828 x exp div}
\psplot[linewidth=1.5pt,linecolor=red,plotpoints=2000]{-2.5}{2.5}{2.71828 x neg exp}
\psline[linestyle=dashed,linewidth=1.25pt](-0.6,-1)(-0.6,9)
\psdots(-0.6,0.656)(-0.6,1.822)
\uput[r](-0.6,0.656){\footnotesize $N$}\uput[r](-0.6,1.822){\footnotesize $M$}
\uput[r](-1.4,7){\blue $\mathcal{C}_f$}\uput[l](-2.1,7.4){\red $\mathcal{C}_g$}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/7.png)
(2.5,\n)}
\multido{\n=-2+1}{5}{\psline[linewidth=0.1pt,linestyle=dashed](\n,-1)(\n,9)}
\psaxes[linewidth=1.25pt,labelFontSize=\scriptstyle,Dy=2]{->}(0,0)(-2.5,-1)(2.5,9)
\psplot[linewidth=1.5pt,linecolor=blue,plotpoints=2000]{-2.5}{2.5}{x dup mul 2.71828 x exp div}
\psplot[linewidth=1.5pt,linecolor=red,plotpoints=2000]{-2.5}{2.5}{2.71828 x neg exp}
\psline[linestyle=dashed,linewidth=1.25pt](-0.6,-1)(-0.6,9)
\psdots(-0.6,0.656)(-0.6,1.822)
\uput[r](-0.6,0.656){\footnotesize $N$}\uput[r](-0.6,1.822){\footnotesize $M$}
\uput[r](-1.4,7){\blue $\mathcal{C}_f$}\uput[l](-2.1,7.4){\red $\mathcal{C}_g$}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/7.png)
-
- Déterminer les coordonnées des points d'intersection de
 et
et 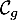 .
.
- Étudier la position relative des courbes
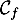 et
et 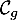 .
.
- Déterminer les coordonnées des points d'intersection de
- Pour tout nombre réel
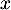 de l'intervalle
de l'intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/13.png) ,
on considère les points
,
on considère les points 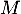 de coordonnées
de coordonnées 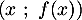 et
et 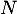 de coordonnées
de coordonnées 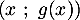 , et on note
, et on note 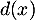 la distance
la distance 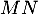 .
On admet que :
.
On admet que :  .
.
On admet que la fonction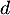 est dérivable sur l'intervalle
est dérivable sur l'intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/22.png) et on note
et on note 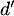 sa fonction dérivée.
sa fonction dérivée.
- Montrer que
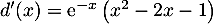 .
.
- En déduire les variations de la fonction
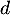 sur l'intervalle
sur l'intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/26.png) .
.
- Déterminer l'abscisse commune
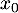 des points
des points  et
et 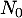 permettant d'obtenir une distance
permettant d'obtenir une distance 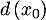 maximale, et donner une valeur approchée à
maximale, et donner une valeur approchée à 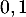 près de la distance
près de la distance 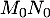 .
.
- Montrer que
- Soit
 la droite d'équation
la droite d'équation 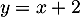 .
.
On considère la fonction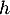 dérivable sur
dérivable sur 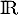 et définie par:
et définie par:
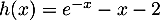 .
.
En étudiant le nombre de solutions de l'équation ,
déterminer le nombre de points d'intersection de la droite
,
déterminer le nombre de points d'intersection de la droite  et de la courbe
et de la courbe 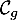 .
.
Correction
Cacher la correction
-
- Les abscisses des points d'intersection de
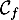 et
et 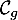 sont les points d'abscisses
sont les points d'abscisses 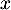 solutions de l'équation
solutions de l'équation 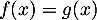 ,
soit
,
soit
![\[f(x)=g(x) \iff x^2e^{-x}=e^{-x}\iff (x^2-1)e^{-x}=0\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/5.png)
Pour tout réel ,
, 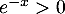 donc en particulier
donc en particulier 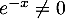 ,
et alors
,
et alors
![\[f(x)=g(x) \iff x^2-1=0 \iff x=-1 \text{ ou } x=1\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/9.png)
Pour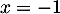 ,
, 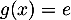 , et pour
, et pour  ,
, 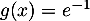 .
.
Les coordonnées des points d'intersection sont donc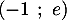 et
et 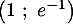 .
.
- Étudier la position relative de
 et
et 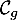 , revient à étudier le signe de
la différence
, revient à étudier le signe de
la différence 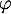 définie par
définie par
![\[\varphi(x)=f(x)-g(x)=(x^2-1)e^{-x}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/19.png)
soit
![\[\renewcommand{\arraystretch}{1.5}
\def\esp{\hspace*{1cm}}
\begin{array}{|c | *7{c} |}
\hline
x & -\infty & \esp & -1 & \esp & 1 & \esp & +\infty \\\hline
x^2-1 & & \pmb{+} & \vline\hspace{-2.7pt}{0} & \pmb{-} & \vline\hspace{-2.7pt}{0} & \pmb{+} &\\\hline
e^{-x} & & \pmb{+} & \vline\hspace{-2.7pt}{\phantom 0} & \pmb{+} & \vline\hspace{-2.7pt}{\phantom 0} & \pmb{+} &\\\hline
(x^2-1)e^{-x} & & \pmb{+} & \vline\hspace{-2.7pt}{0} & \pmb{-} & \vline\hspace{-2.7pt}{0} & \pmb{+} &\\
\hline
\end{array}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/20.png)
Donc sur les intervalles![$]-\infty~;~-1[$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/21.png) et
et ![$]1~;~+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/22.png) ,
la courbe
,
la courbe 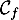 est au dessus de la courbe
est au dessus de la courbe 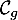 ,
et sur l'intervalle
,
et sur l'intervalle ![$]-1~;~1[$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/25.png) , la courbe
, la courbe 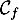 est en dessous
de la courbe
est en dessous
de la courbe 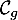 ,
,
- Les abscisses des points d'intersection de
-
- On a
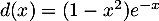 , soit
, soit 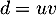 avec
avec 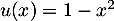 donc
donc 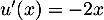 ,
et
,
et 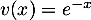 soit
soit 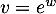 donc
donc 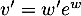 et donc
et donc
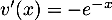 .
On a alors
.
On a alors  , soit
, soit
![\[\begin{array}{ll}d'(x)&=-2xe^{-x}+\lp1-x^2\rp\lp-e^{-x}\rp\\
&=e^{-x}\lp-2x-1+x^2\right)
\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/37.png)
- Dans la dérivée précédente, on a
 pour tout réel
pour tout réel 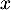 ,
et le trinôme du second degré a pour discriminant
,
et le trinôme du second degré a pour discriminant
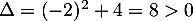 et admet donc deux racines
et admet donc deux racines
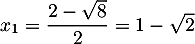 et
et 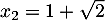 .
.
On a alors
![\[\renewcommand{\arraystretch}{1.5}
\def\esp{\hspace*{0cm}}
\begin{array}{|c | *{11}{c} |} \hline
x & -\infty & \esp & -1 & \esp & 1-\sqrt{2} & \esp & 1 & \esp & 1+\sqrt{2} & \esp & +\infty \\\hline
e^{-x} & & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \vline\hspace{-2.7pt}{\phantom 0} & + &\\\hline
x^2-2x-1& & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \vline\hspace{-2.7pt}{0} & - & \vline\hspace{-2.7pt}{\phantom 0} & - & \vline\hspace{-2.7pt}{0} & + &\\\hline
d'(x)& & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \vline\hspace{-2.7pt}{0} & - & \vline\hspace{-2.7pt}{\phantom 0} & - & \vline\hspace{-2.7pt}{0} & + &\\\hline
&&&&&&&&&&&\\
$d$&&&\psline[arrowsize=7pt]{->}(-.8,-.3)(1,.8)&&&
\psline[arrowsize=7pt]{->}(-.7,.8)(1.4,-.3)&&&&
\psline[arrowsize=7pt]{->}(-.8,-.3)(1,.8)&\\
&&&&&&&&&&&\\\hline
\end{array}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/43.png)
- Sur l'intervalle
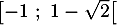 ,
, 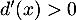 donc
donc  est strictement croissante.
est strictement croissante.
- Sur l'intervalle
![$\left ]1-\sqrt{2}~;~1\right ]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/47.png) ,
, 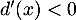 donc
donc 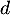 est strictement décroissante.
est strictement décroissante.
- Sur l'intervalle
- D'après la question précédente, la distance
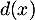 est maximale
pour
est maximale
pour  , et vaut alors
, et vaut alors
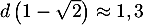
- On a
- On étudie la fonction
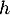 .
.
La fonction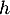 est dérivable, donc continue ssur
est dérivable, donc continue ssur  , avec
, avec
 donc, comme
donc, comme  ,
et donc
,
et donc  et la fonction
et la fonction  est
donc strictement décroissante sur
est
donc strictement décroissante sur  .
.
-
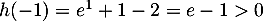 ; comme
; comme 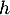 est strictement décroissante,
est strictement décroissante, 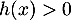 pour
pour 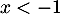 , donc
, donc 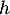 ne s'annule pas sur l'intervalle
ne s'annule pas sur l'intervalle ![$]-\infty~;~-1[$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/66.png) .
.
-
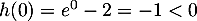 ; comme
; comme  est strictement décroissante,
est strictement décroissante,  pour
pour  , donc
, donc 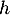 ne s'annule pas sur l'intervalle
ne s'annule pas sur l'intervalle ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/72.png) .
.
- Sur l'intervalle
![$[-1~;~0]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/73.png) , la fonction
, la fonction  est continue et strictement décroissante, et on sait que
est continue et strictement décroissante, et on sait que 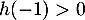 et
et 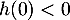 ; donc d'après le corollaire du théorème des valeurs intermédiaires, ou théorème de la bijection,
l'équation
; donc d'après le corollaire du théorème des valeurs intermédiaires, ou théorème de la bijection,
l'équation  admet une solution unique.
admet une solution unique.
La droite et la courbe
et la courbe 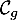 ont donc un unique point d'intersection dont l'abscisse est comprise entre
ont donc un unique point d'intersection dont l'abscisse est comprise entre 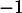 et
et 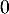 .
.
-
Cacher la correction
Tag:Exponentielle
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
