Bac 2021 (15 mars 2021): exponentielles, distance entre deux courbes
Exercice corrigé - Spécialité maths, terminale générale
Le graphique suivant représente, dans un repère orthogonal, les courbes
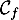 et
et 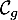 des fonctions
des fonctions  et
et  définies sur
définies sur 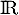 par:
par:
![\[f(x) = x^2e^{-x}\quad \text{ et } \quad g(x) = e^{-x}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/6.png)
(2.5,\n)}
\multido{\n=-2+1}{5}{\psline[linewidth=0.1pt,linestyle=dashed](\n,-1)(\n,9)}
\psaxes[linewidth=1.25pt,labelFontSize=\scriptstyle,Dy=2]{->}(0,0)(-2.5,-1)(2.5,9)
\psplot[linewidth=1.5pt,linecolor=blue,plotpoints=2000]{-2.5}{2.5}{x dup mul 2.71828 x exp div}
\psplot[linewidth=1.5pt,linecolor=red,plotpoints=2000]{-2.5}{2.5}{2.71828 x neg exp}
\psline[linestyle=dashed,linewidth=1.25pt](-0.6,-1)(-0.6,9)
\psdots(-0.6,0.656)(-0.6,1.822)
\uput[r](-0.6,0.656){\footnotesize $N$}\uput[r](-0.6,1.822){\footnotesize $M$}
\uput[r](-1.4,7){\blue $\mathcal{C}_f$}\uput[l](-2.1,7.4){\red $\mathcal{C}_g$}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/7.png)
Correction
(2.5,\n)}
\multido{\n=-2+1}{5}{\psline[linewidth=0.1pt,linestyle=dashed](\n,-1)(\n,9)}
\psaxes[linewidth=1.25pt,labelFontSize=\scriptstyle,Dy=2]{->}(0,0)(-2.5,-1)(2.5,9)
\psplot[linewidth=1.5pt,linecolor=blue,plotpoints=2000]{-2.5}{2.5}{x dup mul 2.71828 x exp div}
\psplot[linewidth=1.5pt,linecolor=red,plotpoints=2000]{-2.5}{2.5}{2.71828 x neg exp}
\psline[linestyle=dashed,linewidth=1.25pt](-0.6,-1)(-0.6,9)
\psdots(-0.6,0.656)(-0.6,1.822)
\uput[r](-0.6,0.656){\footnotesize $N$}\uput[r](-0.6,1.822){\footnotesize $M$}
\uput[r](-1.4,7){\blue $\mathcal{C}_f$}\uput[l](-2.1,7.4){\red $\mathcal{C}_g$}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/7.png)
-
- Déterminer les coordonnées des points d'intersection de
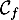 et
et 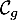 .
.
- Étudier la position relative des courbes
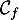 et
et 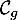 .
.
- Déterminer les coordonnées des points d'intersection de
- Pour tout nombre réel
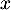 de l'intervalle
de l'intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/13.png) ,
on considère les points
,
on considère les points 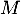 de coordonnées
de coordonnées 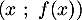 et
et 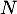 de coordonnées
de coordonnées 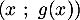 , et on note
, et on note 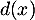 la distance
la distance 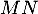 .
On admet que :
.
On admet que :  .
.
On admet que la fonction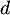 est dérivable sur l'intervalle
est dérivable sur l'intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/22.png) et on note
et on note 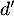 sa fonction dérivée.
sa fonction dérivée.
- Montrer que
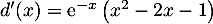 .
.
- En déduire les variations de la fonction
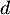 sur l'intervalle
sur l'intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/26.png) .
.
- Déterminer l'abscisse commune
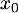 des points
des points  et
et 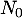 permettant d'obtenir une distance
permettant d'obtenir une distance 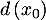 maximale, et donner une valeur approchée à
maximale, et donner une valeur approchée à 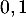 près de la distance
près de la distance 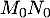 .
.
- Montrer que
- Soit
 la droite d'équation
la droite d'équation 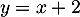 .
.
On considère la fonction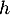 dérivable sur
dérivable sur 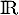 et définie par:
et définie par:
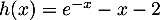 .
.
En étudiant le nombre de solutions de l'équation ,
déterminer le nombre de points d'intersection de la droite
,
déterminer le nombre de points d'intersection de la droite  et de la courbe
et de la courbe 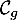 .
.
Correction
Tag:Exponentielle
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
