Bac 2019 (Métropole, septembre) - Intégrale gaussienne, méthode de Monté Carlo
Exercice corrigé - Spécialité maths, terminale générale
On donne ci-dessous la représentation graphique  dans un repère orthogonal d'une fonction
dans un repère orthogonal d'une fonction 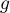 définie et continue sur
définie et continue sur 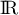 .
La courbe
.
La courbe  est symétrique par rapport à l'axe des ordonnées
et se situe dans le demi-plan
est symétrique par rapport à l'axe des ordonnées
et se situe dans le demi-plan 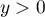 .
.
(\n,1.2)}
\multido{\n=-0.2+0.2}{8}{\psline[linewidth=0.2pt](-2,\n)(2,\n)}
\psaxes[linewidth=1.25pt,Dx=0.5,Dy=0.2](0,0)(-2,-0.19)(2,1.2)
\uput[d](-0.08,-0.02){$0$}
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-2}{2}{1 2.71828 x dup mul exp div}
%\psGauss[mue=0,sigma=0.75,linewidth=1.25pt,linecolor=blue]{-2}{2}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/6.png)
Pour tout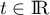 on pose:
on pose:
![\[G(t)=\int_0^t g(u) du\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/8.png)
Partie A
Les justifications des réponses aux questions suivantes pourront s'appuyer sur des considérations graphiques.
Dans la suite du problème, la fonction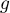 est définie sur
est définie sur 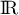 par
par 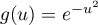 .
.
Partie B
Partie C
On rappelle que la fonction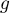 est définie sur
est définie sur 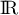 par
par 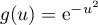 et que la fonction
et que la fonction 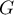 est définie sur
est définie sur 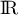 par :
par :
![\[G(t) =\int_0^t g(u) du\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/68.png)
On se propose de déterminer une majoration de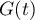 pour
pour 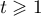 .
.
(\n,1.2)}
\multido{\n=-0.2+0.2}{8}{\psline[linewidth=0.2pt](-2,\n)(2,\n)}
\psaxes[linewidth=1.25pt,Dx=0.5,Dy=0.2](0,0)(-2,-0.19)(2,1.2)
\uput[d](-0.08,-0.02){$0$}
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-2}{2}{1 2.71828 x dup mul exp div}
%\psGauss[mue=0,sigma=0.75,linewidth=1.25pt,linecolor=blue]{-2}{2}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/6.png)
Pour tout
Partie A
Les justifications des réponses aux questions suivantes pourront s'appuyer sur des considérations graphiques.
- La fonction
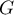 est-elle croissante sur
est-elle croissante sur 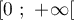 ? Justifier.
? Justifier.
- Justifier graphiquement l'inégalité
 .
.
- La fonction
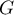 est-elle positive sur
est-elle positive sur 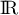 ? Justifier.
? Justifier.
Dans la suite du problème, la fonction
Partie B
- Étude de
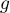
- Déterminer les limites de la fonction
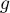 aux bornes
de son ensemble de définition.
aux bornes
de son ensemble de définition.
- Calculer la fonction dérivée de
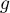 et en déduire
le tableau de variations de
et en déduire
le tableau de variations de 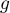 sur
sur 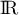 .
.
- Préciser le maximum de
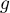 sur
sur 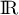 . En déduire que
. En déduire que 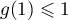 .
.
- Déterminer les limites de la fonction
- On note
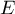 l'ensemble des points
l'ensemble des points 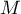 situés entre
la courbe
situés entre
la courbe 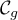 , l'axe des abscisses et les droites d'équation
, l'axe des abscisses et les droites d'équation
 et
et  . On appelle
. On appelle 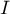 l'aire de cet ensemble.
l'aire de cet ensemble.
On rappelle que:
![\[I=G(1)=\int_0^1 g(u) du\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/31.png)
On souhaite estimer l'aire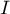 par la méthode dite "de Monte-Carlo"
décrite ci-dessous.
par la méthode dite "de Monte-Carlo"
décrite ci-dessous.
- On choisit un point
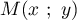 en tirant au hasard de façon
indépendante ses coordonnées
en tirant au hasard de façon
indépendante ses coordonnées 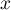 et
et 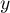 selon la loi uniforme sur
l'intervalle
selon la loi uniforme sur
l'intervalle ![$[0~;~ 1]$](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/36.png) . On admet que la
probabilité que le point
. On admet que la
probabilité que le point 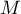 appartienne à l'ensemble
appartienne à l'ensemble 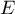 est égale à
est égale à 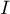 .
.
- On répète
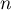 fois l'expérience du choix d'un point
fois l'expérience du choix d'un point 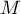 au hasard.
On compte le nombre
au hasard.
On compte le nombre 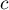 de points appartenant à l'ensemble
de points appartenant à l'ensemble 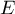 parmi
les
parmi
les 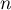 points obtenus.
points obtenus.
- La fréquence
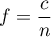 est une estimation de la valeur de
est une estimation de la valeur de 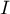 .
.
- La figure ci-dessous illustre la méthode présentée pour
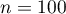 .
Déterminer la valeur de
.
Déterminer la valeur de 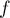 correspondant à ce graphique.
correspondant à ce graphique.
(0,0)(1,1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1}{1 2.71828 x dup mul exp div}
\psdots(0.1,0.98)(0.05,0.02)(0.12,0.9)(0.22,0.83)(0.32,0.82)(0.37,0.815)(0.09,0.76)(0.22,0.69)(0.35,0.67)(0.11,0.7)(0.18,0.53)(0.24,0.63)(0.57,0.61)(0.64,0.61)(0.65,0.6)(0.21,0.58)
(0.48,0.55)(0.64,0.55)(0.66,0.53)(0.7,0.5)(0.57,0.44)(0.72,0.44)(0.77,0.44)(0.85,0.47)
(0.13,0.46)(0.75,0.39)(0.54,0.41)(0.09,0.28)(0.27,0.29)(0.69,0.36)(0.7,0.37)(0.08,0.35)
(0.28,0.28)(0.46,0.25)(0.47,0.23)(0.57,0.28)(0.7,0.28)(0.96,0.25)(0.3,0.23)(0.46,0.23)
(0.54,0.21)(0.93,0.2)(0.96,0.23)(0.025,0.16)(0.035,0.16)(0.18,0.18)(0.28,0.16)(0.41,0.12)
(0.63,0.16)(0.95,0.1)(0.45,0.13)(0.74,0.17)(0.94,0.12)(0.96,0.15)(0.08,0.04)(0.29,0.04)
(0.01,0.02)(0.12,0.02)(0.51,0.01)(0.58,0)(0.92,0)(0.28,0.4)(0.3,0.42)(0.32,0.45)
(0.35,0.5)(0.37,0.55)(0.39,0.57)(0.41,0.5)(0.48,0.41)(0.79,0.2)(0.76,0.15)(0.8,0.1)
(0.85,0.26)(0.9,0.4)(0.44,0.65)(0.44,0.48)(0.57,0.63)
\psdots[dotstyle=o](0.29,0.95)(0.57,0.98)(0.59,0.95)(0.79,0.92)(0.9,0.99)(0.49,0.8)(0.68,0.9)(0.79,0.91)(0.81,0.92)(0.43,0.85)(0.77,0.79)(0.94,0.77)(0.84,0.68)(0.87,0.64)(0.85,0.61)(0.83,0.59)
(0.74,0.77)(0.97,0.69)(0.975,0.495)(0.92,0.47)(0.93,0.44)(0.6,0.8)(0.68,0.78)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/49.png)
- L'exécution de l'algorithme ci-dessous utilise
la méthode de Monte-Carlo décrite précédemment pour déterminer une valeur
du nombre
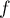 .
Recopier et compléter cet algorithme.
.
Recopier et compléter cet algorithme.
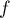 ,
, 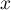 et
et 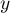 sont des nombres réels,
sont des nombres réels, 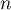 ,
, 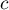 et
et  sont
des entiers naturels.
sont
des entiers naturels.
ALEA est une fonction qui génère aléatoirement un nombre compris entre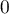 et
et  .
.
![\[\fbox{\begin{minipage}{8cm}
$c \gets 0$\\
Pour $i$ variant de $1$ \`a $n$ faire :\\
\hspace*{2.cm}$x \gets$ ALEA\\
\hspace*{2.cm}$y \gets$ ALEA\\
\hspace*{1cm}Si $y \leqslant \ldots$ alors\\
\hspace*{2.cm}$c \gets \ldots$\\
\hspace*{1cm}fin Si\\
fin Pour\\
\hspace{2.5cm}$f \gets \ldots$\\
\end{minipage}}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/59.png)
- Une exécution de l'algorithme pour
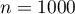 donne
donne 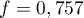 .
En déduire un intervalle de confiance, au niveau de confiance de 95 %,
de la valeur exacte de
.
En déduire un intervalle de confiance, au niveau de confiance de 95 %,
de la valeur exacte de 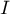 .
.
- On choisit un point
Partie C
On rappelle que la fonction
On se propose de déterminer une majoration de
- Un résultat préliminaire.
On admet que, pour tout réel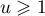 , on a
, on a
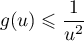 .
.
En déduire que, pour tout réel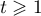 , on a :
, on a :
![\[\int_1^t g(u) du \leqslant 1 - \dfrac1t\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/74.png)
- Montrer que, pour tout réel
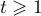 ,
,
![\[G(t) \leqslant 2 - \dfrac1t\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/76.png)
Que peut-on dire de la limite éventuelle de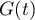 lorsque
lorsque 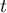 tend vers
tend vers 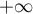 ?
?
Correction
(\n,1.2)}
\multido{\n=-0.2+0.2}{8}{\psline[linewidth=0.2pt](-2,\n)(2,\n)}
\psaxes[linewidth=1.25pt,Dx=0.5,Dy=0.2](0,0)(-2,-0.19)(2,1.2)
\uput[d](-0.08,-0.02){$0$}
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-2}{2}{1 2.71828 x dup mul exp div}
%\psGauss[mue=0,sigma=0.75,linewidth=1.25pt,linecolor=blue]{-2}{2}
\pscustom[fillstyle=vlines]{\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1}{1 2.71828 x dup mul exp div}
\psline(1,0)(0,0)}
\pspolygon[linecolor=red,linewidth=2pt](0,0)(0,1)(0.5,1)(0.5,0.8)(1,0.8)(1,0)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/1.png)
Partie B
Partie C
Cacher la correction
(\n,1.2)}
\multido{\n=-0.2+0.2}{8}{\psline[linewidth=0.2pt](-2,\n)(2,\n)}
\psaxes[linewidth=1.25pt,Dx=0.5,Dy=0.2](0,0)(-2,-0.19)(2,1.2)
\uput[d](-0.08,-0.02){$0$}
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-2}{2}{1 2.71828 x dup mul exp div}
%\psGauss[mue=0,sigma=0.75,linewidth=1.25pt,linecolor=blue]{-2}{2}
\pscustom[fillstyle=vlines]{\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1}{1 2.71828 x dup mul exp div}
\psline(1,0)(0,0)}
\pspolygon[linecolor=red,linewidth=2pt](0,0)(0,1)(0.5,1)(0.5,0.8)(1,0.8)(1,0)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/1.png)
- La fonction
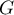 est l'intégrale d'une fonction positive
et est donc croissante sur l'intervalle
est l'intégrale d'une fonction positive
et est donc croissante sur l'intervalle 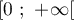 .
.
Algébriquement, on sait que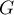 est la primitive de
est la primitive de 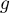 qui s'annule en 1.
On a donc en particulier
qui s'annule en 1.
On a donc en particulier 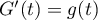 avec
avec 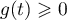 d'après le graphique.
Ainsi,
d'après le graphique.
Ainsi, 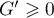 et
et 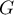 est croissante sur
est croissante sur 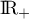 .
.
-
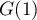 est égale à l'aire, en unités d'aire,
de la surface hachurée sur le graphique.
Cette aire est inférieure à celle des deux rectangles tracés en rouge,
dont l'aire vaut
est égale à l'aire, en unités d'aire,
de la surface hachurée sur le graphique.
Cette aire est inférieure à celle des deux rectangles tracés en rouge,
dont l'aire vaut 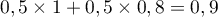 , et on a donc ainsi
, et on a donc ainsi
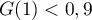 .
.
- Comme
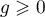 on a, par positivité de l'intégrale, que
pour tout
on a, par positivité de l'intégrale, que
pour tout 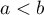 ,
,
![\[\int_a^b g(u)du\geqslant0\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/16.png)
Ainsi, pout tout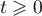 ,
,
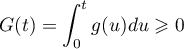 .
.
Par contre, si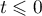 , alors
, alors
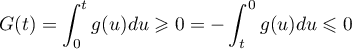 .
.
Ainsi,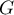 est négative sur
est négative sur 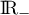 et positive sur
et positive sur 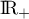 .
.
Partie B
-
- Comme
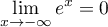 , on a par composition des limites,
, on a par composition des limites,
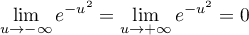 ,
,
c'est-à-dire
![\[\lim_{u\to-\infty} g(u) = \lim_{u \to + \infty} g(u) = 0\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/26.png)
-
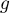 est dérivable sur
est dérivable sur 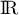 comme composée de la fonction exponentielle
et de la fonction carré, toutes deux dérivables sur
comme composée de la fonction exponentielle
et de la fonction carré, toutes deux dérivables sur 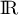 ,
avec,
,
avec,
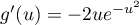 .
.
Comme pour tout réel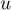 , on a
, on a 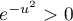 , on a donc
, on a donc
![\[\begin{tabular}{|c|ccccc|}\hline
$u$&$-\infty$&&0&&$+\infty$\\\hline
$-2u$&&$+$&0&$-$&\\\hline
$e^{-u^2}$&&$+$&$|$&$+$&\\\hline
$g'(u)$&&$+$&0&$-$&\\\hline
&&&1&&\\
$g$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&0&&&&0\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/33.png)
- Comme trouvé dans le tableau de variation précédent,
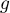 atteint son maximum en
atteint son maximum en 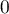 , et qui vaut
, et qui vaut 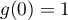 .
Ceci signifie aussi que pour tout réel
.
Ceci signifie aussi que pour tout réel 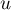 on a
on a 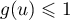 ,
et en particulier pour
,
et en particulier pour  , on a
, on a 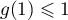 .
.
- Comme
-
- On compte 23 points au dessus de la courbe, donc 77 en dessous,
et donc
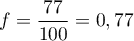 .
.
-
![\[\fbox{\begin{minipage}{8cm}
$c \gets 0$\\
Pour $i$ variant de $1$ \`a $n$ faire :\\
\hspace*{2.cm}$x \gets$ ALEA\\
\hspace*{2.cm}$y \gets$ ALEA\\
\hspace*{1cm}Si $y \leqslant \text{e}^{-x^2}$ alors\\
\hspace*{2.cm}$c \gets c + 1$\\
\hspace*{1cm}fin Si\\
fin Pour\\
\hspace*{2.5cm}$f \gets \dfrac{c}{n}$\\
\end{minipage}}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/42.png)
- Pour
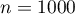 et
et 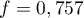 , l'intervalle de confiance
de la valeur exacte de
, l'intervalle de confiance
de la valeur exacte de 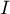 ,
au niveau de confiance de 95 %, est
,
au niveau de confiance de 95 %, est
![\[\left[ f-\dfrac1{\sqrt{n}}~;~f-\dfrac1{\sqrt{n}}\right]
=\bigl[0,725~;~0,789\bigr]\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/46.png)
- On compte 23 points au dessus de la courbe, donc 77 en dessous,
et donc
Partie C
- Comme l'intégrale conserve l'ordre, on a
![\[g(u) \leqslant \dfrac{1}{u^2} \Longrightarrow
\int_1^t g(u) du \leqslant \int_1^t\dfrac{1}{u^2} du\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/47.png)
ce ui nous donne le résultat cherché car
![\[\int_1^t\dfrac{1}{u^2} du=\Bigl[-\dfrac1u\Bigr]_1^t=-\dfrac1t+1\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/48.png)
- On a, en utilisant la relation de Chasles,
![\[\begin{array}{ll}G(t)&=\dsp\int_0^tg(u)du \\[1.2em]
&=\dsp\int_0^1 g(u) du + \int_1^t g(u) du\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/49.png)
Or, on a vu que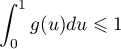 et par ailleurs, dans la question précédente, que
et par ailleurs, dans la question précédente, que
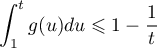 ,
d'où par somme:
,
d'où par somme:
![\[G(t) \leqslant 1+ 1 - \dfrac1t=2-\dfrac1t\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/52.png)
Comme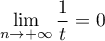 ,
si la limite de
,
si la limite de 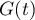 lorsque
lorsque 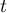 tend vers
tend vers 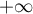 existe, alors
elle est inférieure ou égale à 2.
existe, alors
elle est inférieure ou égale à 2.
Cacher la correction
Tag:Intégrales
Voir aussi:
Quelques devoirs
intégration, Calculs d'intégrales - Suite d'intégrales (Bac S, 19 juin 2014) - Dimensionnement d'un récupérateur d'eau (Bac S - Amérique du nord, 1er juin 2016)
intégration, Calculs d'intégrales - Aire sous une courbe (Bac S - métropole, 11 septembre 2014) - Aire entre deux courbes (Bac S, juin 2008)
sur les intégrales: calcul d'intégrales, suite d'intégrales, et un calcul de volume
sur les intégrales: calcul d'intégrales, suite d'intégrales
