Bac 2014 (Métropole, Septembre) - Exponentielle et intégrales
Exercice corrigé - Spécialité maths, terminale générale
Sur le graphique ci-dessous, on a tracé, dans un repère orthonormé
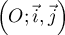 , une courbe
, une courbe 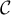 et la droite
et la droite 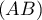 où
où 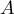 et
et 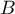 sont les points de coordonnées respectives
sont les points de coordonnées respectives 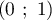 et
et
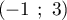 .
.
![\psset{unit=1.2cm,arrowsize=7pt}
\begin{pspicture}(-3,-2.2)(3,3.5)
\psline[linewidth=1pt]{->}(-3,0)(3,0)
\psline[linewidth=1pt]{->}(0,-2.2)(0,3.8)
\rput(0,1){$\tm$}\rput(-1,3){$\tm$}
\uput[ur](0,1){$A$}\uput[l](-1,3){$B$}
\uput[dl](0,0){O}
\psline[linewidth=1.6pt]{->}(0,0)(1,0)\uput[d](0.5,0){$\vec{i}$}
\uput[d](-1,0){$- 1$}\uput[r](0,3){3}
\psline[linewidth=1.6pt]{->}(0,0)(0,1)\uput[l](0,0.5){$\vec{j}$}
\uput[d](-2,-1.2){$\mathcal{C}$}
\psline[linestyle=dashed](-1,0)(-1,3)(0,3)
\psplot[plotpoints=5000,linewidth=1.25pt,linecolor=blue]{-2.5}{2.5}{1 x add x 3 mul 2.71828 x dup mul exp div sub}
\psplot{-1.4}{1.5}{1 x 2 mul sub}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/8.png)
On désigne par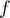 la fonction dérivable sur
la fonction dérivable sur 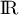 dont la courbe
représentative est
dont la courbe
représentative est 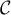 .
.
On suppose, de plus, qu'il existe un réel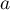 tel que pour tout réel
tel que pour tout réel 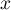 ,
,
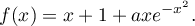
Correction
![\psset{unit=1.2cm,arrowsize=7pt}
\begin{pspicture}(-3,-2.2)(3,3.5)
\psline[linewidth=1pt]{->}(-3,0)(3,0)
\psline[linewidth=1pt]{->}(0,-2.2)(0,3.8)
\rput(0,1){$\tm$}\rput(-1,3){$\tm$}
\uput[ur](0,1){$A$}\uput[l](-1,3){$B$}
\uput[dl](0,0){O}
\psline[linewidth=1.6pt]{->}(0,0)(1,0)\uput[d](0.5,0){$\vec{i}$}
\uput[d](-1,0){$- 1$}\uput[r](0,3){3}
\psline[linewidth=1.6pt]{->}(0,0)(0,1)\uput[l](0,0.5){$\vec{j}$}
\uput[d](-2,-1.2){$\mathcal{C}$}
\psline[linestyle=dashed](-1,0)(-1,3)(0,3)
\psplot[plotpoints=5000,linewidth=1.25pt,linecolor=blue]{-2.5}{2.5}{1 x add x 3 mul 2.71828 x dup mul exp div sub}
\psplot{-1.4}{1.5}{1 x 2 mul sub}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/8.png)
On désigne par
On suppose, de plus, qu'il existe un réel
-
- Justifier que la courbe
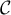 passe par le point
passe par le point 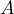 .
.
- Déterminer le coefficient directeur de la droite
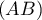 .
.
- Démontrer que pour tout réel
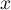 ,
,
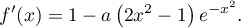
- On suppose que la droite
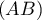 est tangente à la courbe
est tangente à la courbe
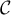 au point
au point 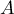 .
.
Déterminer la valeur du réel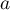 .
.
- Justifier que la courbe
- D'après la question précédente, pour tout réel
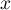 ,
,
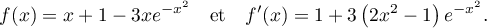
- Démontrer que pour tout réel
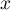 de l'intervalle
de l'intervalle
![$]- 1~;~0]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/27.png) ,
,  .
.
- Démontrer que pour tout réel
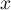 inférieur ou égal à
inférieur ou égal à 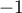 ,
,
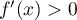 .
.
- Démontrer qu'il existe un unique réel
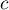 de l'intervalle
de l'intervalle
![$\left[- \dfrac{3}{2}~;~- 1\right]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/33.png) tel que
tel que 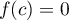 .
Justifier que
.
Justifier que 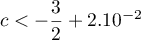 .
.
- Démontrer que pour tout réel
- On désigne par
 l'aire, exprimée en unités d'aire,
du domaine défini par:
l'aire, exprimée en unités d'aire,
du domaine défini par:
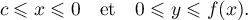
- Écrire
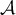 sous la forme d'une intégrale.
sous la forme d'une intégrale.
- On admet que l'intégrale
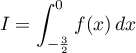 est une valeur approchée de
est une valeur approchée de 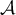 à
à 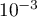 près.
près.
Calculer la valeur exacte de l'intégrale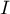 .
.
- Écrire
Correction
Tags:ExponentielleFonctionsIntégrales
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
