Bac 2017 (Antilles-Guyane): exponentielles et tangentes perpendiculaires
Exercice corrigé - Spécialité maths, terminale générale
Soit  et
et  les fonctions définies sur
les fonctions définies sur  par
par
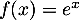 et
et  .
.
On note la courbe représentative de
la courbe représentative de  et
et 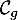 celle de
celle de 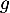 dans un repère orthonormé du plan.
dans un repère orthonormé du plan.
Pour tout réel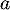 , on note
, on note 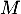 le point de
le point de 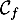 d'abscisse
d'abscisse  et
et 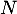 le point de
le point de 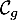 d'abscisse
d'abscisse 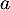 .
.
La tangente en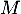 à
à 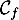 coupe l'axe des abscisses en
coupe l'axe des abscisses en 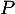 ,
la tangente en
,
la tangente en 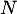 à
à  coupe l'axe des abscisses en
coupe l'axe des abscisses en 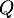 ,
,
On note
Pour tout réel
La tangente en
- Faire une figure représentant la situation.
Que vaut la longueur
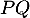 sur cette figure ?
sur cette figure ?
- Démontrer que la tangente en
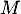 à
à 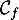 est perpendiculaire
à la tangente en
est perpendiculaire
à la tangente en 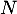 à
à 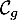 .
.
- Démontrer que, indépendamment de la valeur du réel
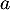 , on a
, on a
 .
.
Correction
D'après Bac Antilles Guyane 2017
Cacher la correction
D'après Bac Antilles Guyane 2017
-
{$\i$}}
\psplot[linewidth=1.6pt]{-5}{3}{2.718 x exp}
\psplot[linewidth=1.6pt]{-3}{5}{2.718 -1 x mul exp}
\psline[linestyle=dashed](.5,0)(!.5\space 2.718 .5 exp)
\rput(.5,-.2){$x$}
\rput(.65,.7){$N$}\rput(.65,1.6){$M$}
\psplot{-3}{3}{2.718 .5 exp x .5 add mul}
\psplot{-3}{3}{2.718 -.5 exp -1 mul x 1.5 sub mul}
\rput(-.45,-.2){$P$}
\rput(1.5,-.2){$Q$}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex-exp-tgt_c/1.png)
-
La tangente en
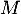 à
à 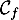 a pour équation
a pour équation
![\[\begin{array}{ll}y&=f'(a)(x-a)+f(a)=e^a(x-a)+e^a\\[.4em]
&=e^ax+e^a(1-a)\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex-exp-tgt_c/4.png)
Une équation cartésienne de cette droite est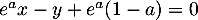 ,
et donc
,
et donc 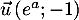 est un vecteur normal à cette droite.
est un vecteur normal à cette droite.
De même, la tangente en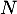 à
à 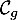 a pour équation
a pour équation
![\[\begin{array}{ll}y&=g'(a)(x-a)+g(a)=-e^{-a}(x-a)+e^{-a}\\[.4em]
&=-e^{-a}x+e^{-a}(1+a)\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex-exp-tgt_c/9.png)
Une équation cartésienne de cette droite est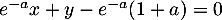 et donc
et donc
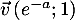 est un vecteur normal à cette droite.
est un vecteur normal à cette droite.
On a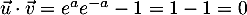 ,
ce qui montre que ces vecteurs sont orthogonaux, comme ces deux tangentes,
qui sont donc perpendiculaires.
,
ce qui montre que ces vecteurs sont orthogonaux, comme ces deux tangentes,
qui sont donc perpendiculaires.
- On détermine les abscisses des points
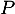 et
et 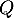 , qui sont à
l'intersection des deux tangentes et de l'axe des abscisses.
, qui sont à
l'intersection des deux tangentes et de l'axe des abscisses.
On a donc, pour le point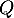 ,
,
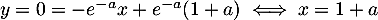 .
.
De même, pour le point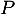 ,
,
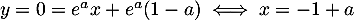 .
.
On en déduit donc que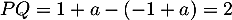 et ne dépend
donc pas de l'abscisse
et ne dépend
donc pas de l'abscisse 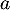 des points
des points 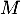 et
et 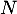 .
.
Cacher la correction
Tag:Exponentielle
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
