Bac 2015 - Géométrie dans l'espace

Exercice corrigé - Spécialité maths, terminale générale

Dans un repère orthonormé (O, I, J, K) d'unité 1 cm, on considère les points , , , .


Un point se déplace sur la droite dans le sens de vers à la vitesse de 1cm par seconde.
Un point se déplace sur la droite dans le sens de vers à la vitesse de 1cm par seconde.
À l'instant le point est en et le point est en .
On note et les positions des points et au bout de secondes, désignant un nombre réel positif.
On admet que et , ont pour coordonnées : et .


Les questions 1 et 2 sont indépendantes.

1. 1. La droite est parallèle à l'un des axes 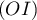, 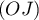ou . Lequel ?
   2. La droite se trouve dans un plan 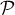parallèle à l'un des plans , 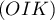ou . Lequel ? On donnera une équation de ce plan .
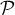   3. Vérifier que la droite 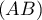, orthogonale au plan 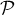, coupe ce plan au point .
   4. Les droites 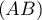et 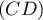sont-elles sécantes ?
2. 1. Montrer que .
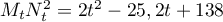   2. À quel instant 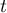la longueur 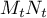est-elle minimale?

Correction

Autres sujets au hasard:

Quelques devoirs

Devoir corrigé
Géométrie plane et exponentielle
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente


Devoir corrigé
Géométrie plane, équation de droites
géométrie plane analytique, vecteurs et équations de droites, géométrie avec une hyperbole et ses tangentes, courbe représentative de la fonction inverse


Devoir corrigé
Géométrie dans l'espace, tangente à une courbe, étude de fonction avec exponentielle
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle


Devoir corrigé
Géométrie dans l'espace - Étude d'une fonction rationnelle
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle - Analyse: étude d'une fonction: variations, limites, TVI, asymptotes, ...


Devoir corrigé
Convexité et géométrie dans l'espace
étude de la convexité de fonctions (et variations, tangentes, limites, ...) et géométrie dans l'espace