Bac 2015 - Géométrie dans l'espace
Exercice corrigé - Spécialité maths, terminale générale
Dans un repère orthonormé (O, I, J, K) d'unité 1 cm, on considère les points
Un point
Un point
À l'instant
On note
On admet que
Les questions 1 et 2 sont indépendantes.
-
- La droite
 est parallèle à l'un des axes
est parallèle à l'un des axes 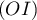 ,
, 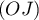 ou
ou  . Lequel ?
. Lequel ?
- La droite
 se trouve dans un plan
se trouve dans un plan 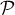 parallèle à l'un des plans
parallèle à l'un des plans  ,
, 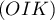 ou
ou  .
Lequel ? On donnera une équation de ce plan
.
Lequel ? On donnera une équation de ce plan 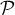 .
.
- Vérifier que la droite
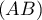 , orthogonale au plan
, orthogonale au plan 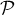 , coupe ce plan au point
, coupe ce plan au point  .
.
- Les droites
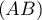 et
et 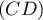 sont-elles sécantes ?
sont-elles sécantes ?
- La droite
-
- Montrer que
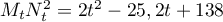 .
.
- À quel instant
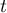 la longueur
la longueur 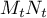 est-elle minimale?
est-elle minimale?
- Montrer que
Correction
Cacher la correction
-
- Un vecteur directeur de la droite
 est
est 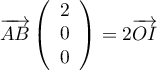 .
La droite
.
La droite  est donc parallèle à l'axe
est donc parallèle à l'axe 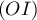 .
.
-
 est un
vecteur directeur de la droite
est un
vecteur directeur de la droite  qui est donc incluse dans un
plan parallèle à
qui est donc incluse dans un
plan parallèle à 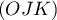
Comme le plan
le plan 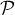 a pour équation cartésienne
a pour équation cartésienne 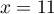 .
.
- On a
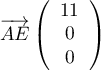 et
et
 , ce qui montre que ces vecteurs
sont colinéaires, et ainsi que
, ce qui montre que ces vecteurs
sont colinéaires, et ainsi que 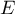 est un point de la droite
est un point de la droite
 .
.
De plus , et donc
, et donc 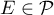 .
.
Ainsi,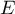 est bien le point d'intersection de
est bien le point d'intersection de 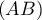 et de
et de 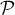 .
.
Remarque: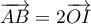 , donc
, donc 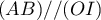 ,
et comme
,
et comme  est parallèle au plan
est parallèle au plan  ,
,
 est bien orthogonale au plan
est bien orthogonale au plan  .
Cette justification n'était par contre pas demandée…
.
Cette justification n'était par contre pas demandée…
-
 est incluse dans
est incluse dans  , et
, et 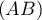 coupe
coupe
 en
en  .
.
Ainsi, si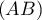 et
et 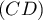 sont sécantes, elles le sont
nécessairement au point
sont sécantes, elles le sont
nécessairement au point 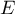 .
.
Or, n'est pas colinéaire à
n'est pas colinéaire à
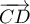 , ce qui montre que
, ce qui montre que 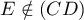 .
.
Ainsi,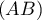 et
et 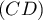 ne sont pas sécantes.
ne sont pas sécantes.
Autre méthode. On peut aussi chercher directement l'éventuelle intersection des deux droites à l'aide de leur représentation paramétrique:

On cherche alors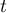 et
et  tels que
tels que
 .
Or ce système n'a pas de solution, et donc
.
Or ce système n'a pas de solution, et donc 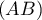 et
et 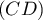 pas
d'intersection et ne sont donc pas sécantes.
pas
d'intersection et ne sont donc pas sécantes.
- Un vecteur directeur de la droite
-
-
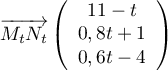 donc
donc 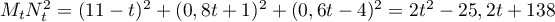 .
.
-
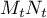 est positif, donc est minimale quand son carré est minimal.
On définit la fonction
est positif, donc est minimale quand son carré est minimal.
On définit la fonction 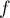 sur
sur 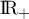 par l'expression
par l'expression
 .
.
 est une fonction du second degré avec
est une fonction du second degré avec
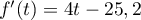 .
.
Ainsi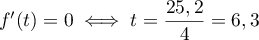 , et
, et 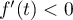 donc
donc 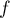 est décroissante pour
est décroissante pour  , et
, et 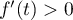 donc
donc 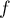 croissante
pour
croissante
pour 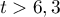 .
.
Ainsi , donc
, donc  , admet un minimum en
, admet un minimum en 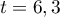 .
.
-
Cacher la correction
Tag:Géométrie dans l'espace
Voir aussi:
