Bac 2014 - Géométrie dans l'espace, dans un tétraèdre…
Exercice corrigé - Spécialité maths, terminale générale
Dans l'espace, on considère un tétraèdre 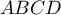 dont les faces
dont les faces 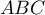 ,
,
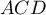 et
et 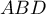 sont des triangles rectangles et isocèles en A.
On désigne par
sont des triangles rectangles et isocèles en A.
On désigne par 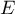 ,
, 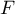 et
et 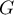 les milieux respectifs des côtés
les milieux respectifs des côtés
![$[AB]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114/8.png) ,
, ![$[BC]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114/9.png) et
et ![$[CA]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114/10.png) .
.
On choisit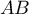 pour unité de longueur et on se place dans le repère
orthonormé
pour unité de longueur et on se place dans le repère
orthonormé 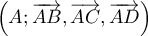 de l'espace.
de l'espace.
Correction
On choisit
- On désigne par
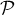 le plan qui passe par A et qui est
orthogonal à la droite (DF).
le plan qui passe par A et qui est
orthogonal à la droite (DF).
On note H le point d'intersection du plan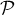 et de la droite (DF).
et de la droite (DF).
- Donner les coordonnées des points D et F.
- Donner une représentation paramétrique de la droite (DF).
- Déterminer une équation cartésienne du plan
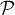 .
.
- Calculer les coordonnées du point H.
- Démontrer que l'angle
 est un angle droit.
est un angle droit.
- On désigne par
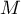 un point de la droite
un point de la droite 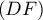 et par
et par 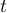 le
réel tel que
le
réel tel que 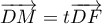 .
On note
.
On note 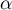 la mesure en radians de l'angle géométrique
la mesure en radians de l'angle géométrique
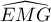 .
.
Le but de cette question est de déterminer la position du point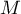 pour que
pour que 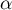 soit maximale.
soit maximale.
- Démontrer que
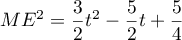 .
.
- Démontrer que le triangle
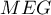 est isocèle en
est isocèle en 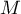 .
En déduire que
.
En déduire que 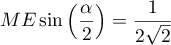 .
.
- Justifier que
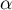 est maximale si et seulement si
est maximale si et seulement si
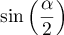 est maximal.
est maximal.
En déduire que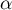 est maximale si et seulement si
est maximale si et seulement si 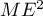 est minimal.
est minimal.
- Conclure.
- Démontrer que
Correction
Tag:Géométrie dans l'espace
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie plane analytique, vecteurs et équations de droites, géométrie avec une hyperbole et ses tangentes, courbe représentative de la fonction inverse
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle - Analyse: étude d'une fonction: variations, limites, TVI, asymptotes, ...
étude de la convexité de fonctions (et variations, tangentes, limites, ...) et géométrie dans l'espace
