Bac 2014 - Géométrie dans l'espace, dans un tétraèdre…
Exercice corrigé - Spécialité maths, terminale générale
Dans l'espace, on considère un tétraèdre 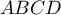 dont les faces
dont les faces 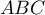 ,
,
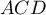 et
et 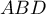 sont des triangles rectangles et isocèles en A.
On désigne par
sont des triangles rectangles et isocèles en A.
On désigne par 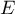 ,
, 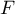 et
et 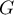 les milieux respectifs des côtés
les milieux respectifs des côtés
![$[AB]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114/8.png) ,
, ![$[BC]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114/9.png) et
et ![$[CA]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114/10.png) .
.
On choisit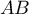 pour unité de longueur et on se place dans le repère
orthonormé
pour unité de longueur et on se place dans le repère
orthonormé 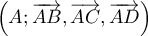 de l'espace.
de l'espace.
On choisit
- On désigne par
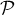 le plan qui passe par A et qui est
orthogonal à la droite (DF).
le plan qui passe par A et qui est
orthogonal à la droite (DF).
On note H le point d'intersection du plan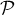 et de la droite (DF).
et de la droite (DF).
- Donner les coordonnées des points D et F.
- Donner une représentation paramétrique de la droite (DF).
- Déterminer une équation cartésienne du plan
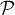 .
.
- Calculer les coordonnées du point H.
- Démontrer que l'angle
 est un angle droit.
est un angle droit.
- On désigne par
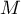 un point de la droite
un point de la droite 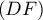 et par
et par 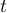 le
réel tel que
le
réel tel que 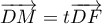 .
On note
.
On note 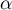 la mesure en radians de l'angle géométrique
la mesure en radians de l'angle géométrique
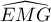 .
.
Le but de cette question est de déterminer la position du point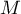 pour que
pour que 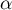 soit maximale.
soit maximale.
- Démontrer que
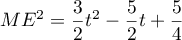 .
.
- Démontrer que le triangle
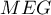 est isocèle en
est isocèle en 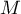 .
En déduire que
.
En déduire que 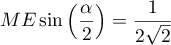 .
.
- Justifier que
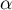 est maximale si et seulement si
est maximale si et seulement si
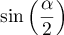 est maximal.
est maximal.
En déduire que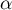 est maximale si et seulement si
est maximale si et seulement si 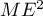 est minimal.
est minimal.
- Conclure.
- Démontrer que
Correction
Tout d'abord, une figure :
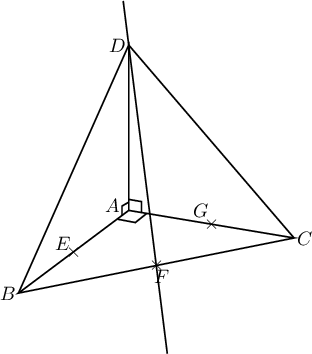
Cacher la correction
Tout d'abord, une figure :

-
- On a
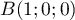 ,
, 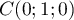 , et
, et 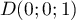 , pour les
coordonnées des points directement liés au repère, et alors
, pour les
coordonnées des points directement liés au repère, et alors
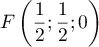 puisque
puisque 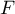 est le milieu de
est le milieu de
![$[BC]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/7.png) .
.
- Une représentation paramétrique de
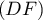 est donnée par
est donnée par
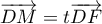 où
où 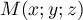 est un point de la droite
de paramètre
est un point de la droite
de paramètre 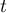 , et
, et
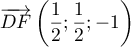 est un vecteur
directeur de la droite.
Cette relation se réécrit sous la forme de la représentation
paramétrique:
est un vecteur
directeur de la droite.
Cette relation se réécrit sous la forme de la représentation
paramétrique:
![$ \la\begin{array}{l}
x=\dfrac{1}{2}t\\[0.3cm]
y = \dfrac{1}{2}t\\[0.3cm]
z = 1 - t\enar\right. t \in \R](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/13.png) .
.
- Le plan
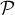 est orthogonal à
est orthogonal à 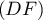 , donc
, donc
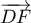 est un vecteur normal à
est un vecteur normal à 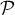 et une équation
cartésienne de
et une équation
cartésienne de 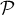 est
est
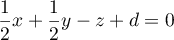 où
où 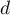 est un réel.
est un réel.
De plus, on sait que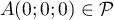 , et donc que
, et donc que
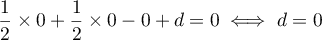 .
.
Ainsi, une équation cartésienne de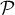 est
est
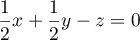
- Le point
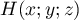 est un point de
est un point de 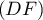 et de
et de 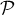 ,
donc ses coordonnées sont celles d'un point de paramètre
,
donc ses coordonnées sont celles d'un point de paramètre 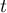 dans
la représentation paramétrique, et qui vérifient également l'équation
du plan: il existe
dans
la représentation paramétrique, et qui vérifient également l'équation
du plan: il existe 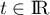 tel que:
tel que:
![$ \la\begin{array}{l}
x=\dfrac{1}{2}t\\[0.3cm]
y = \dfrac{1}{2}t\\[0.3cm]
z = 1 - t\\
\enar\right.](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/30.png) et
et 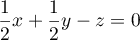 .
.
En substituant les expressions de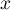 ,
, 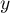 et
et 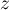 en fonction du
paramètre
en fonction du
paramètre  dans l'équation de
dans l'équation de 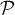 , on obtient:
, on obtient:
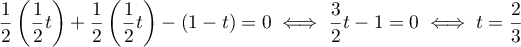
Ainsi,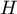 a pour coordonnées
a pour coordonnées
![$ \la\begin{array}{l}
x=\dfrac{1}{2}t=\dfrac12\dfrac23=\dfrac13\\[0.3cm]
y = \dfrac{1}{2}t=\dfrac12\dfrac23=\dfrac13\\[0.3cm]
z = 1 - t=1-\dfrac23=\dfrac13
\enar\right.](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/39.png) ,
c'est à dire:
,
c'est à dire: 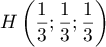 .
.
- Les coordonnées des vecteurs
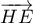 et
et 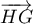 sont:
sont:
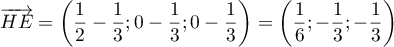 et
et
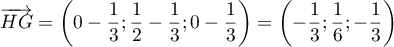 .
.
Comme on travaille avec un repère orthonormé, le produit scalaire des deux vecteurs peut être obtenu avec ces coordonnées, et on a: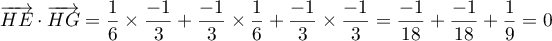 ,
ce qui montre que les vecteurs
,
ce qui montre que les vecteurs 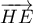 et
et 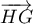 sont
orthogonaux, et donc que l'angle
sont
orthogonaux, et donc que l'angle 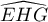 est droit.
est droit.
- On a
- On reconnaît dans le point
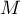 décrit, le point de paramètre
décrit, le point de paramètre 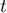 dans la représentation paramétrique de la droite
dans la représentation paramétrique de la droite 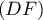 donnée à la
question 1. b..
donnée à la
question 1. b..
- Le point
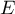 est le milieu du segment
est le milieu du segment ![$[AB]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/53.png) , donc ses
coordonnées sont
, donc ses
coordonnées sont 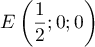 et le
vecteur
et le
vecteur 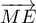 a pour coordonnées:
a pour coordonnées:
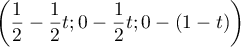 ,
soit
,
soit 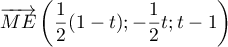 .
.
On a donc
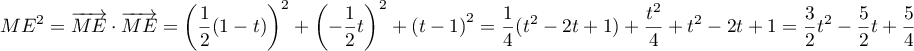
- On procède de façon analogue pour calculer la longueur
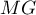 :
Le point
:
Le point 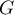 est le milieu du segment
est le milieu du segment ![$[AC]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/61.png) , donc ses coordonnées
sont
, donc ses coordonnées
sont 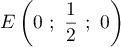 donc le vecteur
donc le vecteur 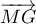 a pour coordonnées:
a pour coordonnées:
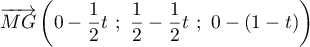 , soit
, soit 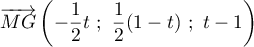 .
.
On a donc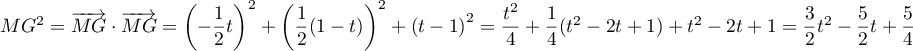 .
.
On a donc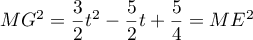 ,
et, comme
,
et, comme 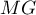 et
et 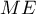 sont des longueurs, donc des nombres
positifs, on a bien
sont des longueurs, donc des nombres
positifs, on a bien 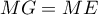 et le triangle
et le triangle 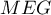 est isocèle.
est isocèle.
Dans le plan , on a la situation:
, on a la situation:
(0,3)
\psline(0,0.3)(0.3,0.3)(0.3,0)
\psarc(0,3){0.65}{245}{270}
\rput(-0.25,2){$\frac{\alpha}{2}$}
\rput(0,-0.2){$I$}
\end{pspicture}](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/73.png)
On a alors, dans le triangle ,
,
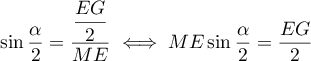 .
Or
.
Or 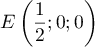 et
et 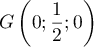 ,
d'où
,
d'où 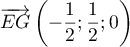 ,
et donc,
,
et donc, 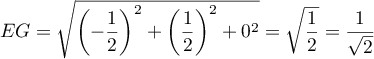 .
On obtient bien ainsi,
.
On obtient bien ainsi,
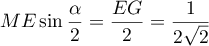 .
.
-
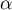 désigne la mesure en radians d'un angle géométrique,
et donc
désigne la mesure en radians d'un angle géométrique,
et donc ![$\alpha\in[0;\pi]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/82.png) .
On a alors
.
On a alors 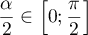 , intervalle sur
lequel la fonction sinus est croissante:
, intervalle sur
lequel la fonction sinus est croissante:
![\begin{tabular}{|c|ccc|}\hline
$\alpha$ & $0$ &\hspace*{1cm}& $\pi$ \\\hline
&&&$\dfrac\pi2$\\
$\dfrac\alpha2$ & &
\psline[arrowsize=7pt]{->}(-.7,-.4)(.8,.5)& \\
&0&&\\\hline
&&&1\\
$\sin\dfrac\alpha2$&&\psline[arrowsize=7pt]{->}(-.7,-.4)(.8,.5)&\\
&0&&\\\hline
\end{tabular}](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/84.png)
On en déduit en particulier que: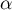 maximal
maximal 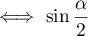 maximal.
maximal.
De plus, on a d'après la question précédente,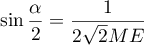 .
.
Donc,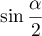 est maximal lorsque
est maximal lorsque 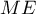 est minimal, et
donc lorsque
est minimal, et
donc lorsque 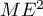 est minimal car la fonction carré étant
croissante sur
est minimal car la fonction carré étant
croissante sur 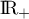 ,
, 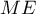 et
et 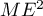 ont le même sens de
variation.
ont le même sens de
variation.
- On avait
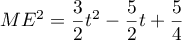 .
En notant
.
En notant 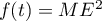 , on définit une fonction
, on définit une fonction 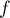 trinôme du
second degré, donc dérivable sur
trinôme du
second degré, donc dérivable sur 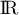 , et telle que
, et telle que
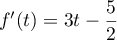 et qui est donc décroissante
sur
et qui est donc décroissante
sur ![$\Bigl[-\infty;\dfrac56\Bigl]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/99.png) et croissante sur
et croissante sur 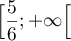 .
En particulier
.
En particulier 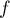 , donc
, donc 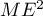 , donc aussi
, donc aussi 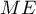 ,
a un minimum en
,
a un minimum en 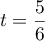 .
.
La position du point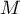 telle que la mesure de l'angle soit
maximale est donc celle atteinte pour le paramètre
telle que la mesure de l'angle soit
maximale est donc celle atteinte pour le paramètre 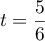 ,
soit
,
soit 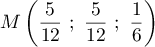 .
.
- Le point
Cacher la correction
Tag:Géométrie dans l'espace
Voir aussi:
