Bac 2012 (Centres étrangers) - Résolution d'une équation avec exponentielle
Exercice corrigé - Spécialité maths, terminale générale
(Bac S, Centres étrangers 2012, 6 points)
On considère l'équation (E) d'inconnue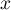 réelle :
réelle :  .
.
Partie A : Conjecture graphique
Le graphique ci-dessous donne la courbe représentative de la fonction exponentielle et celle de la fonction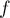 définie sur
définie sur  par
par 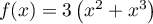 telles que les affiche une calculatrice dans un même repère orthogonal.
telles que les affiche une calculatrice dans un même repère orthogonal.
![\[
\psset{xunit=1.0cm,yunit=1.0cm,algebraic=true,dotstyle=o,dotsize=3pt 0,linewidth=0.8pt,arrowsize=3pt 2,arrowinset=0.25}
\begin{pspicture*}(-7,-6)(7,6)
\psaxes[labelFontSize=\scriptstyle,xAxis=true,yAxis=true,Dx=1,Dy=1,ticksize=-2pt 0,subticks=2]{->}(0,0)(-7,-6)(7,6)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-7.0}{7.0}{EXP(x)}
\psplot[plotpoints=2000,linewidth=1.25pt]{-7.0}{7.0}{3*(x^2+x^3)}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/6.png)
À l'aide du graphique ci-dessus, conjecturer le nombre de solutions de l'équation (E) et leur encadrement par deux entiers consécutifs.
Partie B : étude de la validité de la conjecture graphique
On considère l'équation (E) d'inconnue
Partie A : Conjecture graphique
Le graphique ci-dessous donne la courbe représentative de la fonction exponentielle et celle de la fonction
![\[
\psset{xunit=1.0cm,yunit=1.0cm,algebraic=true,dotstyle=o,dotsize=3pt 0,linewidth=0.8pt,arrowsize=3pt 2,arrowinset=0.25}
\begin{pspicture*}(-7,-6)(7,6)
\psaxes[labelFontSize=\scriptstyle,xAxis=true,yAxis=true,Dx=1,Dy=1,ticksize=-2pt 0,subticks=2]{->}(0,0)(-7,-6)(7,6)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-7.0}{7.0}{EXP(x)}
\psplot[plotpoints=2000,linewidth=1.25pt]{-7.0}{7.0}{3*(x^2+x^3)}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/6.png)
À l'aide du graphique ci-dessus, conjecturer le nombre de solutions de l'équation (E) et leur encadrement par deux entiers consécutifs.
Partie B : étude de la validité de la conjecture graphique
-
- Étudier selon les valeurs de
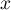 , le signe de
, le signe de  .
.
- En déduire que l'équation (E)n'a pas de solution sur l'intervalle
![$]-\infty~;~-1]$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/9.png) .
.
- Vérifier que 0 n'est pas solution de (E).
- Étudier selon les valeurs de
- On considère la fonction
 , définie pour tout nombre réel de
, définie pour tout nombre réel de ![$]-1~;~0[\cup]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/11.png) par :
par :
![\[h(x)=\ln 3+\ln\left(x^2\right)+\ln(1+x)-x.\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/12.png)
Montrer que, sur![$]-1~;~0[\: \cup\: ]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/13.png) , l'équation (E) équivaut à
, l'équation (E) équivaut à 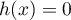 .
.
-
- Etudier les limites de
 en
en 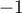 ,
, 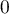 et
et 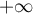 .
.
- Montrer que, pour tout réel
 appartenant à
appartenant à ![$]-1~;~0[~\cup~]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/20.png) , on a:
, on a:
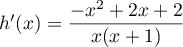
- Déterminer les variations de la fonction
 .
.
- Déterminer le nombre de solutions de l'équation
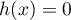 et donner une valeur arrondie au centième de chaque solution.
et donner une valeur arrondie au centième de chaque solution.
- Conclure quant à la conjecture de la partie A.
- Etudier les limites de
Correction
(Bac S, Centres étrangers 2012, 6 points)
Partie A: Conjecture. Les solutions de l'équation (E) sont les abscisses des points d'intersection des deux courbes. Il semble y en avoir 2. L'une comprise entre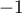 et
et  , l'autre entre 0 et 1.
, l'autre entre 0 et 1.
Partie B : étude de la validité de la conjecture graphique
Cacher la correction
(Bac S, Centres étrangers 2012, 6 points)
Partie A: Conjecture. Les solutions de l'équation (E) sont les abscisses des points d'intersection des deux courbes. Il semble y en avoir 2. L'une comprise entre
Partie B : étude de la validité de la conjecture graphique
-
-
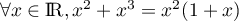 ,
avec
,
avec 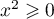 et
et 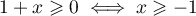 , ainis
, ainis
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ &$-\infty$ && $-1$ && $0$ && $+\infty$\\\hline
$x^2$ && $+$ &$|$&$+$&\zb&$+$& \\\hline
$1+x$ && $-$ &\zb&$+$&$|$&$+$& \\\hline
$x^3+x^2$ && $-$ &\zb&$+$&\zb&$+$& \\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/6.png)
- On a donc, pour tout
 ,
, 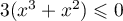 .
Or,
.
Or, 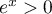 pour tout
pour tout 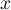 réel, et donc il ne peut pas y avoir de
solution
réel, et donc il ne peut pas y avoir de
solution 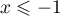 à (E)
à (E)
-
 et
et 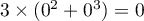 . Donc
. Donc 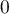 n'est pas solution de (E).
n'est pas solution de (E).
-
-
![$\forall x \in ]-1~;~0[~\cup~]0~;~+\infty[,
\begin{array}[t]{lcl}
\mbox{(E)} & \iff & e^x=3(x^2+x^3) \\
&\iff & \ln e^x=\ln\left( 3(x^2+x^3)\right) \\
&\iff & x=\ln3+\ln\left( x^2( 1+x) \right) \\
&\iff & x=\ln3+\ln\left( x^2 \right) + \ln\left(1+x\right) \\
&\iff & \ln3 + \ln\left( x^2 \right) + \ln\left( 1+x\right) -x = 0
\iff h(x) = 0 \\
\end{array} $](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/15.png)
-
- En
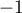 :
:  ,
et, par composition,
,
et, par composition,
 ,
et alors, par additions,
,
et alors, par additions,
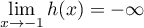 .
.
En : par composition,
: par composition,
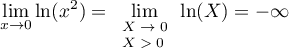 ,
et
,
et 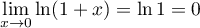 .
.
Ainsi, par addition, .
.
En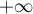 : On a, pour tout
: On a, pour tout  ,
,
![$h(x)=\ln3-x\Bigl[-2\dfrac{\ln(x)}{x}-\dfrac{\ln(1+x)}{x}+1\Bigr]$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/26.png) .
.
De plus, par croissances comparées,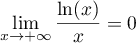 ,
et donc aussi
,
et donc aussi
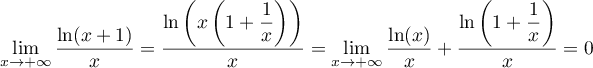 ,
,
On a alors, par addition et produit,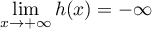 .
.
-
 est une somme et composée de fonctions de référence dérivables, donc
est une somme et composée de fonctions de référence dérivables, donc 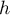 est bien dérivable sur
est bien dérivable sur ![$]-1~;~0[~\cup~]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/32.png) .
.
Plus précisément, pour tout réel![$x\in]-1;0[\cup]0;+\infty[,$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/33.png) on a
on a
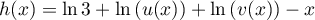 ,
,
avec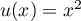 , donc
, donc  , et
, et 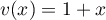 , donc
, donc 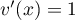 ,
et ainsi,
,
et ainsi,
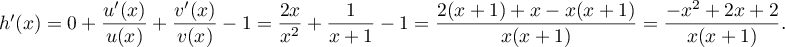
- Le numérateur de
 est un trinôme du second degré qui a
pour discriminant
est un trinôme du second degré qui a
pour discriminant 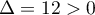 et qui admet donc deux racines
et qui admet donc deux racines 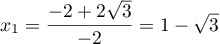 et
et  .
.
Le dénominateur est aussi un trinôme du second degré dont les racines sont mises en évidence: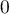 et
et 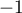 .
.
![\[\begin{tabular}{|c|ccccccccc|}\hline
$x$ & $-1$ && $1-\sqrt{3}$ && $0$&& $ 1+\sqrt{3} $&&$+\infty$\\\hline
$-x^2+2x+2$ && $-$ & $0$ && $+$ & &$0$
&$-$&\\\hline $x(x+1)$ & $0$ && $-$&&$0$ & &$+$ &&\\\hline
$h'(x)$ & $\mid\mid$ & $+$ & $0$ &$-$ &$\mid\mid$&$ + $ &$ 0 $ &$-$& \\\hline
&&&&&&&&&\\
$h$&
\psline(0,.8)(0,-.6)\,\psline(0,.8)(0,-.6)&
\psline[arrowsize=7pt]{->}(-.2,-.3)(.7,.4)
&&
\psline[arrowsize=7pt]{->}(-.7,.4)(.3,-.3)
&
\psline(0,.8)(0,-.6)\,\psline(0,.8)(0,-.6)&
\psline[arrowsize=7pt]{->}(-.2,-.3)(.7,.4)
&&
\psline[arrowsize=7pt]{->}(-.7,.4)(.3,-.3)
&
\\
&\qquad\ \scriptsize$-\infty$\hspace*{-2em}&&&\quad\scriptsize$-\infty$\hspace*{-2em}
&\qquad\ \scriptsize$-\infty$\hspace*{-2em}&&&\quad\scriptsize$-\infty$\hspace*{-3em}&
\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/46.png)
-
- Sur l'intervalle
![$ ]-1;0[ $](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/47.png) ,
, 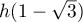 est un maximum pour
est un maximum pour  .
Or
.
Or 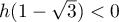 donc l'équation
donc l'équation 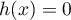 n'a pas de solution sur
n'a pas de solution sur ![$]-1;0[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/52.png) .
C'est une première contradiction avec la conjecture de la partie A.
.
C'est une première contradiction avec la conjecture de la partie A.
- Sur l'intervalle
![$ ]0 ~;~ 1+\sqrt{3}[ $](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/53.png) la fonction
la fonction 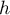 est
dérivable, donc continue, strictement croissante, et
est
dérivable, donc continue, strictement croissante, et  est compris entre
est compris entre
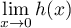 et
et 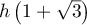 , d'après le théorème
de la bijection, l'équation
, d'après le théorème
de la bijection, l'équation 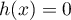 admet une unique solution
admet une unique solution
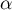 sur
sur 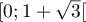 .
.
La calculatrice donne: et
et
 ,
et donc
,
et donc  .
On trouve de même que
.
On trouve de même que 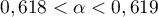 Une valeur approchée de
Une valeur approchée de 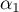 , arrondie au centième est donc
, arrondie au centième est donc 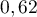 .
.
- De même sur
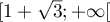 , où
, où 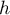 est continue et
strictement décroissante, on aune unique solution
est continue et
strictement décroissante, on aune unique solution 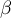 ,
avec, à l'aide de la calculatrice,
,
avec, à l'aide de la calculatrice,

- Sur l'intervalle
- La conjecture émise à la partie A était fausse: il y a bien deux solutions mais pas là où on les pensait.
- En
Cacher la correction
Tag:Exponentielle
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
