Bac 2011 (Amérique du nord) - Étude de fonctions avec exponentielle, position relative, suite récurrente
Exercice corrigé - Spécialité maths, terminale générale
Partie A
On considère la fonction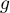 définie sur
définie sur 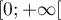 par
par
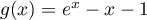 .
.
Partie B
On considère la fonction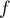 définie sur
définie sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/11.png) par
par
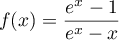 .
.
La courbe représentative de la fonction
représentative de la fonction  dans le plan muni
d'un repère orthonormal est donnée en annexe.
Cette annexe sera complétée et remise avec la copie à la fin de
l'épreuve.
dans le plan muni
d'un repère orthonormal est donnée en annexe.
Cette annexe sera complétée et remise avec la copie à la fin de
l'épreuve.
On admet que est strictement croissante sur
est strictement croissante sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/16.png) .
.
Partie C
On considère la suite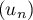 définie par:
définie par:
![$\la\begin{array}{ll} u_0=\dfrac12 \\[0.3cm] \text{pour tout entier naturel } n, u_{n+1}=f\left( u_n\rp\enar\right.](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/35.png) .
.
Annexe
Cette page sera complétée et remise avec la copie à la fin de l'épreuve.
![\psset{unit=5cm,arrowsize=7pt}
\fbox{\begin{pspicture}(-.2,-.2)(1.5,1.5)
\psline[linewidth=1.6pt]{->}(-.2,0)(1.5,0)
\psline[linewidth=1.6pt]{->}(0,-.2)(0,1.5)
\psplot{0}{1}{2.718 x exp 1 sub 2.718 x exp x sub div}
\newcommand{\f}[1]{#1 10 div}
\multido{\i=-2+1}{18}{
\psline[linewidth=.8pt,linestyle=dotted](!\f{\i}\space-.2)(!\f{\i}\space1.5)
\psline[linewidth=.8pt,linestyle=dotted](!-.2\space\f{\i})(!1.5\space\f{\i})
}
\rput(-.05,-.05){$O$}
\psline(1,-.02)(1,.02)\rput(1,-.08){$1$}
\psline(-.02,1)(.02,1)\rput(-.08,1){$1$}
\rput(.9,1.05){$(C)$}
\end{pspicture}}](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/39.png)
On considère la fonction
- Etudier les variations de la fonction
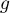 .
.
- Déterminer le signe de
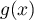 suivant les valeurs de
suivant les valeurs de 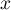 .
.
- En déduire que pour tout
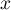 de
de  ,
, 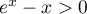 .
.
Partie B
On considère la fonction
La courbe
On admet que
- Montrer que pour tout
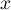 de
de ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/18.png) ,
, ![$f(x)\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/19.png) .
.
- Soit
 la droite d'équation
la droite d'équation 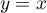 .
.
- Montrer que pour tout
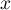 de
de ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/23.png) ,
, 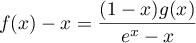 .
.
- Etudier la position relative de la droite
 et de la
courbe
et de la
courbe 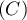 sur
sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/27.png) .
.
- Montrer que pour tout
-
- Déterminer une primitive de
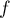 sur
sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/29.png) .
.
- Calculer l'aire, en unité d'aire, du domaine du plan délimité
par la courbe
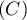 , la droite
, la droite  et les droites d'équations
et les droites d'équations
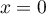 et
et  .
.
- Déterminer une primitive de
Partie C
On considère la suite
![$\la\begin{array}{ll} u_0=\dfrac12 \\[0.3cm] \text{pour tout entier naturel } n, u_{n+1}=f\left( u_n\rp\enar\right.](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/35.png) .
.
- Construire sur l'axe des abscisses les quatre premiers termes de la suite en laissant apparents les traits de construction.
- Montrer que pour tout entier
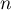 ,
,
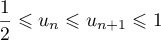 .
.
- En déduire que la suite
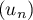 est convergente et
déterminer sa limite.
est convergente et
déterminer sa limite.
Annexe
Cette page sera complétée et remise avec la copie à la fin de l'épreuve.
![\psset{unit=5cm,arrowsize=7pt}
\fbox{\begin{pspicture}(-.2,-.2)(1.5,1.5)
\psline[linewidth=1.6pt]{->}(-.2,0)(1.5,0)
\psline[linewidth=1.6pt]{->}(0,-.2)(0,1.5)
\psplot{0}{1}{2.718 x exp 1 sub 2.718 x exp x sub div}
\newcommand{\f}[1]{#1 10 div}
\multido{\i=-2+1}{18}{
\psline[linewidth=.8pt,linestyle=dotted](!\f{\i}\space-.2)(!\f{\i}\space1.5)
\psline[linewidth=.8pt,linestyle=dotted](!-.2\space\f{\i})(!1.5\space\f{\i})
}
\rput(-.05,-.05){$O$}
\psline(1,-.02)(1,.02)\rput(1,-.08){$1$}
\psline(-.02,1)(.02,1)\rput(-.08,1){$1$}
\rput(.9,1.05){$(C)$}
\end{pspicture}}](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/39.png)
Correction
Partie A On considère la fonction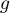 définie sur
définie sur 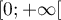 par
par
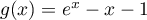 .
.
Partie B
Partie C
Cacher la correction
Partie A On considère la fonction
-
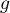 est la somme de la fonction exponentielle et d'une fonction
affine et est donc dérivable sur
est la somme de la fonction exponentielle et d'une fonction
affine et est donc dérivable sur 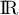 , donc sur
, donc sur 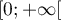 ,
avec,
,
avec, 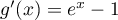 .
.
De plus, la fonction exponentielle est strictement croissante sur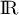 , lorsque
, lorsque ![$x\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/9.png) , on a
, on a 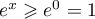 , et
donc
, et
donc 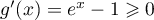 .
.
On a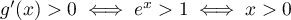 , car
Ainsi, on a le tableau de variation:
, car
Ainsi, on a le tableau de variation:
![\begin{tabular}{|c|cccc|}\hline
$x$ & $0$ &\hspace*{1cm}& &$+\infty$ \\\hline
$g'(x)$ &$0$& $+$ &&\\\hline
&&&&\\
$g$&&\psline[arrowsize=6pt]{->}(-.6,-.2)(1,.4)&&\\
&$0$&&&\\\hline
\end{tabular}](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/13.png)
- Comme
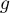 est strictement croissante sur
est strictement croissante sur 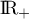 et que
et que 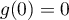 ,
on en déduit que pour tout
,
on en déduit que pour tout 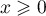 ,
,
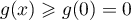 .
.
- On a donc pour tout
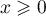 ,
,
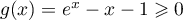 ,
et ainsi,
,
et ainsi,  .
.
Partie B
- Comme
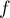 est strictement croissante sur
est strictement croissante sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/23.png) ,
on a
,
on a ![$x\in[0;1]\iff 0\leqslant x\leqslant 1\iff f(0)\leqslant f(x)\leqslant f(1)](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/24.png) .
.
Or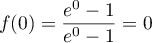 et
et 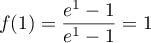 ,
et on a donc bien ainsi
,
et on a donc bien ainsi ![$0\leqslant f(x)\leqslant 1 \iff f(x)\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/27.png) .
.
- Soit
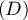 la droite d'équation
la droite d'équation 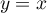 .
.
- Pour tout
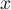 de
de ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/31.png) ,
,
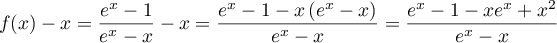 .
.
Or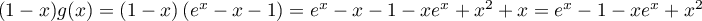 .
.
On a donc ainsi bien, pour tout![$x\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/34.png) ,
,
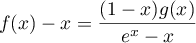 .
.
- On a vue que, pour tout
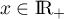 , donc aussi tout
, donc aussi tout
![$x\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/37.png) ,
, 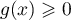 et
et 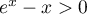 .
.
Ainsi,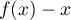 est du même signe que
est du même signe que 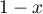 , et donc
, et donc
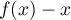 est positif sur
est positif sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/43.png) :
la courbe
:
la courbe 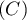 est au dessus de la droite
est au dessus de la droite 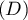 sur
sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/46.png) ,
,
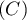 et
et 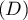 se coupant en
se coupant en 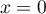 (car
(car 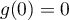 ) et en
) et en 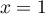 .
.
- Pour tout
-
-
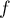 est de la forme
est de la forme 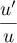 , avec
, avec 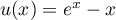 .
.
Comme, pour![$x\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/55.png) ,
, 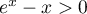 , d'après la partie A, une
primitiver de
, d'après la partie A, une
primitiver de 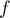 est donc
est donc
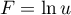 , soit
, soit 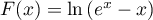 .
.
- L'aire du domaine est:
![\begin{array}{ll}\mathcal{A}&\dsp=\int_0^1\!\!\Bigl( f(x)-x\Bigr)\,dx
=\int_0^1\!\!f(x)\,dx-\int_0^1\!\!x\,dx
=\Bigl[F(x)\Bigr]_0^1-\Bigl[\dfrac12x^2\Bigr]_0^1\\[0.3cm]
&\dsp=\Bigl(F(1)-F(0)\Bigr)- \Bigl(\dfrac121^2-\dfrac120^2\Bigr)
=\ln(e-1)-\dfrac12\enar](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/60.png)
-
Partie C
-
![\psset{unit=5cm,arrowsize=7pt}
\fbox{\begin{pspicture}(-.2,-.2)(1.5,1.5)
\psline[linewidth=1.6pt]{->}(-.2,0)(1.5,0)
\psline[linewidth=1.6pt]{->}(0,-.2)(0,1.5)
\newcommand{\f}[1]{2.718 #1 exp 1 sub 2.718 #1 exp #1 sub div}
\psplot{0}{1}{\f{x}}
\newcommand{\fr}[1]{#1 10 div}
\multido{\i=-2+1}{18}{
\psline[linewidth=.8pt,linestyle=dotted](!\fr{\i}\space-.2)(!\fr{\i}\space1.5)
\psline[linewidth=.8pt,linestyle=dotted](!-.2\space\fr{\i})(!1.5\space\fr{\i})
}
\rput(-.05,-.05){$O$}
\psline(1,-.02)(1,.02)\rput(1,-.08){$1$}
\psline(-.02,1)(.02,1)\rput(-.08,1){$1$}
\rput(.9,1.05){$(C)$}
% Construction des termes de la suite
\psplot{-0.2}{1.2}{x}
\newcommand\fn[2]{%
\ifnum#1=1
\f{#2}%
\else
\f{\fn{\numexpr#1-1}{#2}}%
\fi
}
% Valeur initiale (u_0)
\def\xinit{0.5}
\def\nmax{3}
% Initialisation pour u_0
\psline[linestyle=dashed]
(\xinit,0)
(!\xinit\space\f{\xinit})
(!\f{\xinit}\space\f{\xinit})
\rput(\xinit,-0.06){$u_0$}
% Boucle pour u_1, u_2, ..., u_nmax
\multido{\i=1+1}{\nmax}{
\psline[linestyle=dashed]
(!\fn{\i}{\xinit} \space 0)
(!\fn{\i}{\xinit} \space \fn{\i}{\xinit})
(!\fn{\i}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
(!\fn{\numexpr\i+1}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
\rput(!\fn{\i}{\xinit}\space 0){$\tm$}
\rput(!\fn{\i}{\xinit}\space -0.06){$u_\i$}
}
\end{pspicture}}](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/61.png)
- Montrons par récurrence que pour tout entier
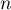 ,
,
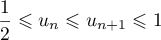 .
.
Initialisation: Pour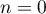 , on a
, on a 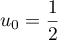 et
et 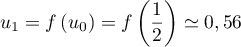 , et donc on a bien
, et donc on a bien 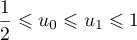 .
.
Hérédité: Supposons que pour un certain entier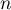 , on ait
, on ait
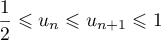 , alors,
comme la fonction
, alors,
comme la fonction 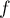 est strictement croissante sur
est strictement croissante sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/71.png) , on a
donc
, on a
donc
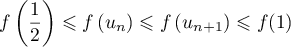 ,
,
soit aussi, comme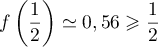 ,
,
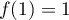 , et
, et 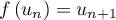 et
et 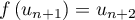 ,
,
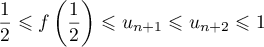 ,
,
ce qui montre que la propriété est encore vraie au rang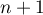 .
.
Conclusion: On vient donc de démontrer d'après le principe de récurrence que pour tout entier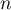 ,
,
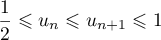 .
.
- D'après le résultat précédent, la suite
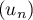 est
croissante et majorée par 1, elle est donc convergente vers une
limite
est
croissante et majorée par 1, elle est donc convergente vers une
limite 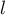 .
.
Comme la fonction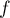 est continue sur
est continue sur 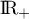 (car elle y est même
dérivable), on a alors
(car elle y est même
dérivable), on a alors
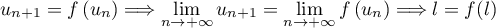
La limite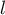 est donc une solution de l'équation
est donc une solution de l'équation 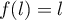 (c'est
aussi le théorème du point fixe), et il s'agit donc de l'abscisse
d'un point d'intersection de
(c'est
aussi le théorème du point fixe), et il s'agit donc de l'abscisse
d'un point d'intersection de 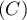 et
et 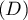 ,
soit
,
soit 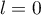 ou
ou 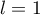 d'après la question 2.b) de la partie B.
d'après la question 2.b) de la partie B.
Or, d'après la question précédente, pour tout entier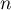 ,
,
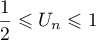 , et donc
, et donc 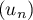 est minorée
par
est minorée
par  et ne peut pas converger vers
et ne peut pas converger vers 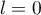 .
.
Ainsi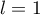 , et la suite
, et la suite 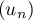 converge donc vers 1.
converge donc vers 1.
Cacher la correction
Tags:ExponentielleSuites
Voir aussi:
