Intégration par parties


On ne sait pas toujours trouver une primitive d'une fonction donnée: tout simplement parce que toutes les fonctions n'ont en pas forcément sous forme simple et explicite.
La formule d'intégration par parties peut alors être utilisée, en permettant de transformer une intégrale de manière à ce que, on espère, la nouvelle forme soit plus facilement calculable.


Primitives

Chapitre précédent et prérequis sur les primitives.

Calcul d'intégrales


Chapitre précédent et prérequis sur le .

Intégration par parties


Théorème
Soit $u$ et $v$ deux fonctions définies, dérivables et dont les dérivées sont continues sur un intervalle $[a,b]$, alors
\[\int_a^b u(x)v'(x)dx = \Bigl[ u(x)v(x)\Bigr]_a^b-\int_a^bu'(x)v(x)dx\]

ou encore, dans une forme moins rigoureuse mais plus simple à mémoriser:
\[\int_a^buv'=\Bigl[uv\Bigr]_a^b-\int_a^bu'v\]

C'est un théorème dont il est bon de connaître la démonstration, car elle permet, entre autre, de pouvoir mémoriser la formule plus simplement et de l'appliquer correctement.



En pratique, lorsqu'on doit intégrer un produit, le formule d'intégration par parties permet de décomposer celui-ci: une des deux fonctions va être dérivée (et donc, on espère, simplifier lel calcul), et il faut connaître une primitive de l'autre.


Exercice 1
Calculer les intégrales suivantes:
a) $\dsp I=\int_0^3 xe^x\,dx$
On pose
\[\la\bgar{ll}u=x\\v'=e^x\enar\right. \text{ donc } \la\bgar{ll}u'=1\\v=e^x\enar\right.\]

et alors, l'intégration par parties donne
\[\bgar{ll}I&=\dsp\int_0^3uv'\\[.8em] &=\Bigl[uv\Bigr]_0^3-\dsp\int_0^3u'v\\[.8em] &=\Bigl[xe^x\Bigr]_0^3-\dsp\int_0^3e^x\,dx\\[.8em] &=\Bigl(3e^3-0\Bigr)-\Bigl[e^x\Bigr]_0^3\\[.8em] &=3e^3-\Bigl(e^3-e^0\Bigr)\\[.6em] &=2e^3+1\enar\]



b) $\dsp J=\int_{-2}^2 4xe^{3x-1}dx$
On pose
\[\la\bgar{ll}u=4x\\v'=e^{3x-1}\enar\right. \text{ donc } \la\bgar{ll}u'=4\\v=\dfrac13e^{3x-1}\enar\right.\]

et alors, l'intégration par parties donne
\[\bgar{ll}J&=\dsp\int_{-2}^2uv' =\Bigl[uv\Bigr]_{-2}^2-\int_{-2}^2u'v\\[.8em] &=\Bigl[4x\dfrac13e^{3x-1}\Bigr]_{-2}^2-\dsp\int_{-2}^24\dfrac13e^x\,dx\\[1.2em] &=\lp\dfrac83e^5-\lp-\dfrac38e^{-7}\rp\rp-\lb\dfrac49e^{3x-1}\rb_{-2}^2\\[1em] &=\dfrac83e^5+\dfrac83^{-7}-\lp\dfrac49e^5-\dfrac49e^{-7}\rp\\[1em] &=4\lp\dfrac59e^5+\dfrac79e^{-7}\rp\enar\]



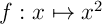
c) $\dsp K=\int_{-1}^1 2x(8x+2)^2dx$
Ici, nul besoin d'une intégration par parties: on peut soit développer et obtenir un polynôme de degré 3 et donc facile à intégrer:
\[\bgar{ll}K&=\dsp\int_{-1}^12x\lp64x^2+32x+4\rp\,dx\\[1em] &=\dsp\int_{-1}^1\lp128x^3+64x^2+8x\rp\,dx\\[1em] &=\lb32x^4+\dfrac{64}3x^3+4x^2\rb_{-1}^1\\[1.2em] &=\lp32+\dfrac{64}3+4\rp -\lp32-\dfrac{64}3+4\rp\\[1em] &=\dfrac{128}3 \enar\]

On peut aussi intégrer par parties avec
\[\la\bgar{ll}u=2x\\v'=(8x+2)^2\enar\right. \text{ donc } \la\bgar{ll}u'=2\\v=\dfrac1{24}(8x+2)^3\enar\right.\]

qui permet, bien sûr et normalement, d'arriver au même résultat.



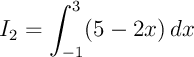
d) $\dsp L=\int_{-1}^1 2x^3e^{x^2-1}dx$
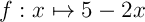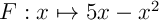On ne connaît pas de primitive de $x\mapsto e^{x^2-1}$, mais par contre on la connaît pour $x\mapsto 2xe^{x^2-1}$.
On décompose donc
\[L=\int_{-1}^1 x^2\tm2xe^{x^2-1}\,dx\]

On pose donc
\[\la\bgar{ll}u=x^2\\v'=2xe^{x^2-1}\enar\right. \text{ donc } \la\bgar{ll}u'=2x\\v=e^{x^2-1}\enar\right.\]

et alors, l'intégration par parties donne
\[\bgar{ll}L&=\dsp\int_{-1}^1uv' =\Bigl[uv\Bigr]_{-1}^1-\int_{-1}^1u'v\\[.8em] &=\Bigl[x^2e^{x^2-1}\Bigr]_{-1}^1-\dsp\int_{-1}^12xe^{x^2-1}\,dx\\[.8em] &=\Bigl(e^0-e^0\Bigr)-\Bigl[e^{x^2-1}\Bigr]_{-1}^1\\[1em] &=-\lp e^0-e^0\rp\\ &=0 \enar\]


Remarque: On aurait pu (dû ?) remarquer dès le début que la fonction à intégrer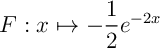 $f:x\mapsto 2x^3e^{x^2-1}$ est impaire, donc sa courbe représentative est symétrique par rapport à l'origine du repère, et donc que les aires entre cette courbe et l'axe des abscisses sur les intervalles $[-1;0]$ et $[0;1]$ sont opposées (égales en valeur absolue, et de signes contraires), et donc l'aire algbrique totale est nulle.



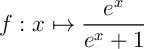
e) $\dsp M=\int_0^1 x^2e^xdx$
On pose
\[\la\bgar{ll}u=x^2\\v'=e^x\enar\right. \text{ donc } \la\bgar{ll}u'=2x\\v=e^x\enar\right.\]

et alors, l'intégration par parties donne
\[\bgar{ll}M&=\dsp\int_0^1uv' =\Bigl[uv\Bigr]_0^1-\int_0^1u'v\\[.8em] &=\Bigl[x^2e^x\Bigr]_0^1-\dsp\int_0^12xe^x\,dx\\[.8em] &=e-\dsp\int_0^12xe^x\,dx \enar\]

Il nous reste encore cette dernière intégrale à calculer: par parties aussi !
On pose maintenant
\[\la\bgar{ll}u=2x\\v'=e^x\enar\right. \text{ donc } \la\bgar{ll}u'=2\\v=e^x\enar\right.\]

et alors, l'intégration par parties donne
\[\bgar{ll}M&=e-\dsp\int_0^1uv'\\[.8em] &=e-\lp\Bigl[uv\Bigr]_0^1-\dsp\int_0^1u'v\rp\\[.8em] &=e-\Bigl[2xe^x\Bigr]_0^1+\dsp\int_0^12e^x\,dx\\[.8em] &=e-\lp 2e-0\rp+\Bigl[2e^x\Bigl]_0^1\,dx\\[1em] &=e-2 \enar\]

Voir, et faire, aussi: autres exercices de calculs d'intégrales par IPP


Exercice 2
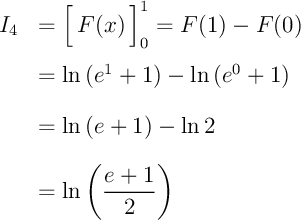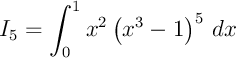On considère les intégrales $\dsp I=\int_0^{\frac{\pi}{2}} e^x \sin(x)\,dx$ et $\dsp J=\int_0^{\frac{\pi}{2}} e^x \cos(x)\,dx$.


  1. En appliquant de deux façons différentes à l'intégrale 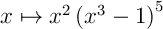$I$ la méthode d'intégration par parties, trouver deux relation entre 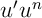$I$ et $J$.

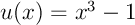  2. Calculer alors les intégrales 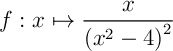$I$ et $J$.



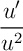Exercice 3
Pour tout entier naturel 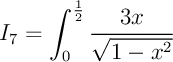$n$, on pose $\dsp I_n=\int_0^\pi x^2\cos(nx)\,dx$.
À l'aide d'une double intégration par parties, calculer $I_n$ en fonction de $n$.



Exercice 4
Soit 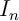$(I_n)$ la suite définie pour tout entier $n\geq0$ par $\dsp I_n=\int_0^1 t^n\,e^{-t}\,dt$.
  1. Calcul des premiers termes de la suite
    1. Calculer 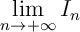$I_0$ et $I_1$.
      On peut calculer directement ces intégrales à l'aide de primitives.

    2. Exprimer 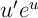$I_2$ en fonction de $I_1$, puis en déduire $I_2$.
      Intégrer par parties pour, en le dérivant, diminuer la puissance du facteur $t^2$
    3. Exprimer $I_3$ en fonction de $I_2$, puis calculer $I_3$.
      De même que dans la question précédente: intégrer par parties pour, en le dérivant, diminuer la puissance du facteur $t^3$


  2. Étude de la suite
    1. Démontrer que, pour tout entier $n$, $I_n\geq 0$.
      positivité de l'intégrale…

    2. Étudier le sens de variation de la suite $(I_n)$.
      Comme pour toute suite, signe de $I_{n+1}-I_n$ ?
      Signe, donc, d'une intégrale: positivité de l'intégrale ?
    3. Démontrer que la suite $(I_n)$ est convergente.
      Convergence monotone ?


  3. Calcul de la limite de la suite
    1. À l'aide d'une intégration par parties, exprimer $I_{n+1}$ en fonction de $I_n$.
      Cas générale des questions 1.b) et 1.c)
    2. Démontrer que, pour tout entier $n\geq 1$, $\dsp I_n\leqslant \dfrac{1}{n}$.
      Pour majorer (ou minorer, ou encadrer) une intégrale, on majore (ou minore, ou encadre) la fonction à intégrer, puis on peut passer aux intégrales comme l'intgégrale conserve l'ordre.
    3. En déduire la limite de la suite $(I_n)$.
      D'après 2.a) la suite est minorée par …, donc avec la question précédente, elle est encadrée par …
      Gendarmes ?!


Voir aussi:
LongPage: h2: 3 - h3: 0