Calcul intégral
Primitives
Chapitre précédent et prérequis: primitives, et calculs de primitives (exercices corrigés).Calcul d'intégrales
Rappel de la propriété fondamentale, précisant le lien entre intégrale (et donc calcul d'aire) et primitive:
Théorème
Soit Alors la fonction
![\[F(x)=\int_a^x f(t)\,dt\]](Cours-IMG/6.png)
Exercice 1
Soit ![\[F(x)=\int_0^x \dfrac{1}{1+t^2}\,dt\]](Cours-IMG/11.png)
Une conséquence directe de ce théorème est la formule fondamentale pour le calcul d'intégrales:
Corollaire
Soit ![\[\bgar{ll}
\dsp\int_a^bf(x)\,dx
&=\Bigl[\,F(x)\,\Bigr]_a^b\\[1em]
&=F(b)-F(a)\enar\]](Cours-IMG/24.png)
Exercice 2
Calculer les intégrales suivantes:
a)
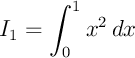
Une primitive de 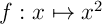 est
est 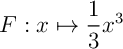 et on a donc
et on a donc
![\[\bgar{ll}I_1&=\Bigl[\,F(x)\,\Bigr]_0^1
=F(1)-F(0)\\[1em]
&=\dfrac13\tm1^3-\dfrac13\tm0^3\\[1em]
&=\dfrac13\enar\]](Cours-IMG/28.png)
![\[\bgar{ll}I_1&=\Bigl[\,F(x)\,\Bigr]_0^1
=F(1)-F(0)\\[1em]
&=\dfrac13\tm1^3-\dfrac13\tm0^3\\[1em]
&=\dfrac13\enar\]](Cours-IMG/28.png)
b)
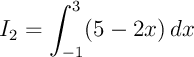
Une primitive de 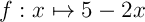 est
est 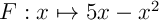 et on a donc
et on a donc
![\[\bgar{ll}I_2&=\Bigl[\,F(x)\,\Bigr]_{-1}^3
=F(3)-F(-1)\\[1em]
&=\Bigl(5\tm3-3^2\Bigr)-\Bigl(5\tm(-1)-(-1)^2\Bigr)\\[1em]
&=12\enar\]](Cours-IMG/32.png)
![\[\bgar{ll}I_2&=\Bigl[\,F(x)\,\Bigr]_{-1}^3
=F(3)-F(-1)\\[1em]
&=\Bigl(5\tm3-3^2\Bigr)-\Bigl(5\tm(-1)-(-1)^2\Bigr)\\[1em]
&=12\enar\]](Cours-IMG/32.png)
c)
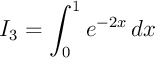
Une primitive de 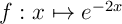 est
est 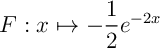 et on a donc
et on a donc
![\[\bgar{ll}I_3&=\Bigl[\,F(x)\,\Bigr]_0^1
=F(1)-F(0)\\[1em]
&=\lp-\dfrac12e^{-2}\rp-\lp-\dfrac12e^0\rp\\[1em]
&=\dfrac12\lp1-e^{-2}\rp\enar\]](Cours-IMG/36.png)
![\[\bgar{ll}I_3&=\Bigl[\,F(x)\,\Bigr]_0^1
=F(1)-F(0)\\[1em]
&=\lp-\dfrac12e^{-2}\rp-\lp-\dfrac12e^0\rp\\[1em]
&=\dfrac12\lp1-e^{-2}\rp\enar\]](Cours-IMG/36.png)
d)
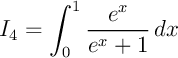
La fonction 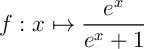 est de la forme
est de la forme
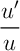 avec
avec 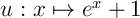 ,
et
,
et 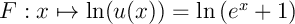 est donc une primitive de
est donc une primitive de 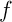 et on a donc
et on a donc
![\[\bgar{ll}I_4&=\Bigl[\,F(x)\,\Bigr]_0^1
=F(1)-F(0)\\[1em]
&=\ln\lp e^1+1\rp-\ln\lp e^0+1\rp\\[1em]
&=\ln\lp e+1\rp-\ln2\\[1em]
&=\ln\lp\dfrac{e+1}2\rp\enar\]](Cours-IMG/43.png)
![\[\bgar{ll}I_4&=\Bigl[\,F(x)\,\Bigr]_0^1
=F(1)-F(0)\\[1em]
&=\ln\lp e^1+1\rp-\ln\lp e^0+1\rp\\[1em]
&=\ln\lp e+1\rp-\ln2\\[1em]
&=\ln\lp\dfrac{e+1}2\rp\enar\]](Cours-IMG/43.png)
e)
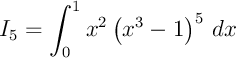
On peut penser à développer l'expression, encore faut-il savoir développer
l'identité remarquable avec une puissance 5 (c'est alors la formule du binôme de Newton).
Plus facilement, la fonction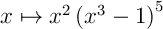 est de la forme
est de la forme
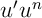 avec
avec 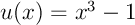 et
et
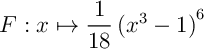 est donc une primtive de
est donc une primtive de 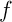 et on a donc
et on a donc
![\[\bgar{ll}I_5&=\Bigl[\,F(x)\,\Bigr]_0^1
=F(1)-F(0)\\[1em]
&=\dfrac1{18}\lp1^3-1\rp^6-\dfrac1{18}\lp0^3-1\rp^6\\[1em]
&=-\dfrac1{18}\enar\]](Cours-IMG/50.png)
Plus facilement, la fonction
![\[\bgar{ll}I_5&=\Bigl[\,F(x)\,\Bigr]_0^1
=F(1)-F(0)\\[1em]
&=\dfrac1{18}\lp1^3-1\rp^6-\dfrac1{18}\lp0^3-1\rp^6\\[1em]
&=-\dfrac1{18}\enar\]](Cours-IMG/50.png)
f)
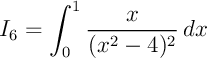
La fonction 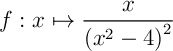 est de la forme
est de la forme
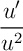 avec
avec 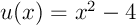 ,
et
,
et 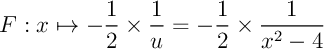 est donc une primitive de
est donc une primitive de 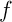 et on a donc
et on a donc
![\[\bgar{ll}I_6&=\Bigl[\,F(x)\,\Bigr]_0^1
=F(1)-F(0)\\[1em]
&=-\dfrac12\tm\dfrac1{1^2-4}-\lp-\dfrac12\tm\dfrac1{0^2-4}\rp\\[1em]
&=\dfrac16-\dfrac18=\dfrac1{24}\enar\]](Cours-IMG/57.png)
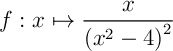 est de la forme
est de la forme
![\[\bgar{ll}I_6&=\Bigl[\,F(x)\,\Bigr]_0^1
=F(1)-F(0)\\[1em]
&=-\dfrac12\tm\dfrac1{1^2-4}-\lp-\dfrac12\tm\dfrac1{0^2-4}\rp\\[1em]
&=\dfrac16-\dfrac18=\dfrac1{24}\enar\]](Cours-IMG/57.png)
g)
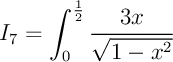
La fonction 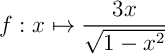 est de la forme
est de la forme
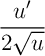 avec
avec 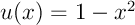 ,
et
,
et 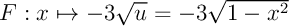 est donc une primitive de
est donc une primitive de 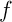 et on a donc
et on a donc
![\[\bgar{ll}I_6&=\Bigl[\,F(x)\,\Bigr]_0^{1/2}
=F\lp\dfrac12\rp-F(0)\\[1em]
&=-3\sqrt{1-\lp\dfrac12\rp^2}-\lp-3\sqrt{1-0^2}\rp\\[1.2em]
&=-3\sqrt{\dfrac34}+3
=-\dfrac{3\sqrt3}2+3\\[1.2em]
\enar\]](Cours-IMG/64.png)
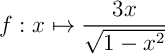 est de la forme
est de la forme
![\[\bgar{ll}I_6&=\Bigl[\,F(x)\,\Bigr]_0^{1/2}
=F\lp\dfrac12\rp-F(0)\\[1em]
&=-3\sqrt{1-\lp\dfrac12\rp^2}-\lp-3\sqrt{1-0^2}\rp\\[1.2em]
&=-3\sqrt{\dfrac34}+3
=-\dfrac{3\sqrt3}2+3\\[1.2em]
\enar\]](Cours-IMG/64.png)
Voir, et faire, aussi: autres exercices de calculs d'intégrales et primitives
Exercice 3
On considère la fonction 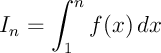 .
.
- Dresser le tableau de variation de
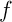 et tracer l'allure de
sa courbe représentative.
et tracer l'allure de
sa courbe représentative.
Représenter sur ce graphique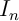 .
.
Les variations sont données par le signe de la dérivée. Ici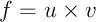 avec
avec 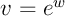 …
…
L'intégrale est, une fois l'allure de la courbe tracée, l'aire du domaine sous la courbe entre les abscisses donées par les bornes de l'intégrale.
- Calculer
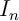 pour tout entier, puis déterminer
pour tout entier, puis déterminer
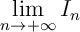
La fonction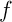 a intégrer est de la forme
a intégrer est de la forme 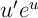 …
…
Pour la suite on rappelle que
Propriété
La valeur moyenne d'une fonction continue (ou continue par morceaux)
définie sur ![\[\mu=\dfrac1{b-a}\int_a^bf(x)\,dx\]](Cours-IMG/106.png)
Exercice 4
Calculer la valeur moyenne des fonctions suivantes sur l'intervalle
a)
Une primitive de 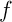 est
est 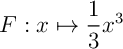 et donc
et donc
![\[\bgar{ll}\mu&=\dfrac1{1-(-1)}\dsp\int_{-1}^1f(x)dx\\[1.2em]
&=\dfrac12\Bigl[\,F(x)\,\Bigr]_{-1}^1\\[1em]
&=\dfrac12\Bigl(F(1)-F(-1)\Bigr)\\[1em]
&=\dfrac12\lp\dfrac13\tm1^3-\dfrac13(-1)^3\rp\\[1em]
&=\dfrac13\enar\]](Cours-IMG/112.png)
![\[\bgar{ll}\mu&=\dfrac1{1-(-1)}\dsp\int_{-1}^1f(x)dx\\[1.2em]
&=\dfrac12\Bigl[\,F(x)\,\Bigr]_{-1}^1\\[1em]
&=\dfrac12\Bigl(F(1)-F(-1)\Bigr)\\[1em]
&=\dfrac12\lp\dfrac13\tm1^3-\dfrac13(-1)^3\rp\\[1em]
&=\dfrac13\enar\]](Cours-IMG/112.png)
b)
Une primitive de 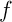 est
est 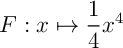 et donc
et donc
![\[\bgar{ll}\mu&=\dfrac1{1-(-1)}\dsp\int_{-1}^1f(x)dx\\[1.2em]
&=\dfrac12\Bigl[\,F(x)\,\Bigr]_{-1}^1\\[1em]
&=\dfrac12\Bigl(F(1)-F(-1)\Bigr)\\[1em]
&=\dfrac12\lp\dfrac14\tm1^4-\dfrac13(-1)^4\rp\\[1em]
&=0\enar\]](Cours-IMG/117.png)
Remarque: ce résultat était prévisible car la fonction cube est impaire, et donc, sa courbe est symétrique par rapport à l'origine du repère, et sa valeur moyenne sur un intervalle centré sur 0 est donc nulle.
![\[\bgar{ll}\mu&=\dfrac1{1-(-1)}\dsp\int_{-1}^1f(x)dx\\[1.2em]
&=\dfrac12\Bigl[\,F(x)\,\Bigr]_{-1}^1\\[1em]
&=\dfrac12\Bigl(F(1)-F(-1)\Bigr)\\[1em]
&=\dfrac12\lp\dfrac14\tm1^4-\dfrac13(-1)^4\rp\\[1em]
&=0\enar\]](Cours-IMG/117.png)
Remarque: ce résultat était prévisible car la fonction cube est impaire, et donc, sa courbe est symétrique par rapport à l'origine du repère, et sa valeur moyenne sur un intervalle centré sur 0 est donc nulle.
c)
En développant, 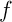 est un polynôme de degré 5, donc facile à intégrer.
est un polynôme de degré 5, donc facile à intégrer.
Plus facilement ici, on remarque que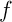 est de la forme
est de la forme
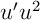 avec
avec 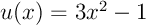 , et donc que
, et donc que
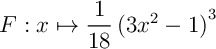 est une primitive de
est une primitive de 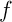 ,
et alors
,
et alors
![\[\bgar{ll}\mu&=\dfrac1{2-(-1)}\dsp\int_{-1}^2f(x)\,dx\\[1em]
&=\dfrac13\Bigl[\,F(x)\,\Bigr]_{-1}^2\\[1em]
&=\dfrac14\Bigl(F(2)-F(-1)\Bigr)\\[1em]
&=\dfrac13\lp\dfrac1{18}\lp3\tm2^2-1\rp^3-\dfrac1{18}\lp3\tm(-1)^2-1\rp^3\rp\\[1em]
&=24,5
\enar\]](Cours-IMG/126.png)
Plus facilement ici, on remarque que
![\[\bgar{ll}\mu&=\dfrac1{2-(-1)}\dsp\int_{-1}^2f(x)\,dx\\[1em]
&=\dfrac13\Bigl[\,F(x)\,\Bigr]_{-1}^2\\[1em]
&=\dfrac14\Bigl(F(2)-F(-1)\Bigr)\\[1em]
&=\dfrac13\lp\dfrac1{18}\lp3\tm2^2-1\rp^3-\dfrac1{18}\lp3\tm(-1)^2-1\rp^3\rp\\[1em]
&=24,5
\enar\]](Cours-IMG/126.png)
d)
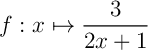 sur
sur ![\[\bgar{ll}\mu=&\dfrac1{4-0}\dsp\int_0^4f(x)\,dx\\[1em]
&=\dfrac14\Bigl[\,F(x)\,\Bigr]_0^4\\[1em]
&=\dfrac14\Bigl(F(4)-F(0)\Bigr)\\[1em]
&=\dfrac14\lp\dfrac32\ln(2\tm4+1)-\dfrac32\ln(2\tm0+1)\rp\\[1em]
&=\dfrac38\ln9=\dfrac34\ln3
\enar\]](Cours-IMG/134.png)
e)
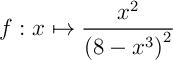 sur
sur ![\[\bgar{ll}\mu&=\dfrac1{1-0}\dsp\int_0^1f(x)\,dx\\[1em]
&=\Bigl[\,F(x)\,\Bigr]_0^1\\[1em]
&=F(1)-F(0)\\[1em]
&=\dfrac13\tm\dfrac1{8-1^3}-\dfrac13\tm\dfrac1{8-0^3}\\[1em]
&=\dfrac1{3\tm7\tm8}=\dfrac1{168}
\enar\]](Cours-IMG/142.png)
f)
![\[\bgar{ll}\mu&=\dfrac1{1-(-1)}\dsp\int_{-1}^1f(x)\,dx\\[1em]
&=\dfrac12\Bigl[\,F(x)\,\Bigr]_{-1}^1\\[1em]
&=\dfrac12\Bigl(F(1)-F(-1)\Bigr)\\[1em]
&=\dfrac12\lp-\dfrac13e^{-2}+\dfrac13e^4\rp\\[1em]
&=\dfrac16\lp e^4-e^{-2}\rp
\enar\]](Cours-IMG/150.png)
Exercice 5
Dans un repère orthonormé, on considère le domaine Déterminer l'aire du domaine
(On pourra se rappeler que
![\[\psset{unit=3cm,arrowsize=5pt}
\begin{pspicture}(-.15,-.15)(1.15,1.25)
\nwc\f[1]{#1 0.5 exp}\nwc\g[1]{#1 #1 mul}
\pscustom{\psplot[plotpoints=100]{0}{1}{\f{x}}\gsave
\psplot[plotpoints=100]{1}{0}{\g{x}}\fill[fillstyle=solid,fillcolor=gray]\grestore}
\psplot[plotpoints=100]{0}{1}{\f{x}}
\psplot[plotpoints=100]{0}{1}{\g{x}}
\psline{->}(-0.1,0)(1.25,0)
\psline{->}(0,-0.1)(0,1.15)
\psline[linestyle=dashed](0,1)(1,1)(1,0)
\rput(-0.08,-0.08){$O$}
\rput(1,-0.08){$1$}\rput(-0.08,1){$1$}
\end{pspicture}\]](Cours-IMG/157.png)
Exercice 6
Calculer l'aire du domaine compris entre les courbes des fonctions
![\[\psset{xunit=.7cm,yunit=.6cm,arrowsize=5pt,arrowsize=8pt}
\begin{pspicture}(-2.5,-4.2)(2.6,2.6)
\nwc\f[1]{#1 2 exp 4 sub}
\nwc\g[1]{#1 2 exp -.5 mul 2 add}
\pscustom{
\psplot{-2}{2}{\f{x}}\gsave
\psplot{2}{-2}{\g{x}}
\fill[fillstyle=solid,fillcolor=lightgray]
\grestore}
%
\psline{->}(-2.5,0)(2.7,0)
\psline{->}(0,-4.3)(0,2.7)
\psplot{-2}{2}{\f{x}}
\psplot{2}{-2}{\g{x}}
\end{pspicture}\]](Cours-IMG/174.png)
Exercice 7
Étude d'une suite (D'après Bac)
On considère la fonction
![\[u_0=\int_0^1 f(x)\,dx\]](Cours-IMG/187.png)
et, pour tout entier
![\[u_n=\int_0^1 x^n\,f(x)\,dx\]](Cours-IMG/189.png)
-
- Démontrer que, pour tout réel
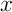 de l'intervalle
de l'intervalle ![$[0;1]$](Cours-IMG/191.png) ,
on a
,
on a 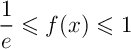 .
.
Dresser le tableau de variation de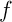 ,
ou manipuler les encadrements à partir de
,
ou manipuler les encadrements à partir de
![$x\in[0;1]\iff 0\leqslant x\leqslant1$](Cours-IMG/194.png) .
.
- En déduire que
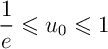 .
.
L'intégrale conserve l'ordre…
- Démontrer que, pour tout réel
- Calculer
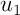 .
.
Dérivée de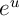 ?
? -
- Démontrer que, pour tout entier naturel
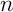 ,
on a
,
on a 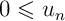 .
.
Positivité de l'intégrale…
- Etudier les variations de la suite
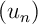 .
.
En déduire que la suite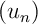 est convergente.
est convergente.
Signe de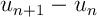 ?
?
- Démontrer que, pour tout entier naturel
-
- Démontrer que, pour tout entier naturel
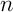 ,
on a
,
on a 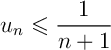 .
.
Utiliser la majoration de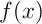 trouvée en 1. a),
d'où
trouvée en 1. a),
d'où 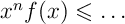 ,
et enfin comme l'intégrale conserve l'ordre…
,
et enfin comme l'intégrale conserve l'ordre…
- En déduire la limite de la suite
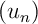 .
.
Encadrement de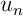 ? Gendarmes ?!
? Gendarmes ?!
- Démontrer que, pour tout entier naturel
Exercice 8
D'après Bac
On considère la suite numérique
![\[ J_n=\int_1^n e^{-t}\,\sqrt{1+t}\,dt\,.\]](Cours-IMG/247.png)
- Démontrer que la suite
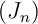 est croissante.
est croissante.
Signe de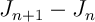 ?
?
- On définit la suite
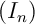 , pour tout entier naturel
, pour tout entier naturel 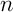 non nul,
par:
non nul,
par:
![\[I_n=\dsp\int_1^n (t+1)\,e^{-t}\,dt\]](Cours-IMG/252.png)
- Justifier que, pour tout
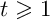 , on a
, on a
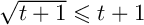 .
.
On élève au carré ces nombres positifs…
- En déduire que
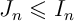 .
.
en multipliant par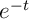 l'inégalité précédente, puis comme l'intégrale conserve l'ordre…
l'inégalité précédente, puis comme l'intégrale conserve l'ordre…
- Déterminer deux réels
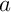 et
et 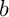 tels que
la fonction
tels que
la fonction 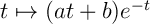 soit une primitive de la
fonction
soit une primitive de la
fonction 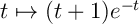 .
.
Exprimer alors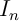 en fonction de
en fonction de 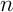 .
.
Dériver la fonction proposée et identifier les coefficients.
- En déduire que la suite
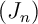 est majorée par un nombre réel.
est majorée par un nombre réel.
D'après les deux résultats précédents b) et c)…
- Que peut-on en conclure pour la suite
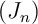 ?
?
Suite croissante et majorée, questions 1) et 2.d)
- Justifier que, pour tout
Intégration par parties
Chapitre suivant: intégration par parties (IPP) pour le calcul d'intégralesVoir aussi: