Tableaux de signes et intersection de deux courbes
Exercice corrigé - maths en seconde générale
Énoncé
Soit 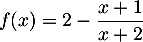 et
et 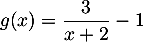 .
.
- Donner les tableaux de signe de
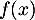 et de
et de 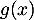 .
.
- Déterminer les coordonnées des éventuels points d'intersection des courbes de
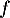 et de
et de 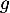 .
.
Correction
Correction
- Sur le même dénominateur, on a
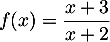 et
et 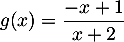 puis les tableaux de signe:
puis les tableaux de signe:
![\[\begin{tabular}[t]{|c|ccccccc|}\hline
$x$&$-\infty$ & & $-3$ & & $-2$ & & $+\infty$ \\\hline
$x+3$ & & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ &\\\hline
$x+2$ & & $-$ & $|$ & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline
$f(x)$ & & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} & $+$ & \\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap3/exTSinter_c/3.png)
et
![\[\begin{tabular}[t]{|c|ccccccc|}\hline
$x$&$-\infty$ & & $-2$ & & $1$ & & $+\infty$ \\\hline
$-x+1$ & & $+$ & $|$ & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline
$x+2$ & & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ &\\\hline
$g(x)$ & & $-$ & \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap3/exTSinter_c/4.png)
- Soit
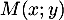 un éventuel point d'intersection des deux courbes,
alors
un éventuel point d'intersection des deux courbes,
alors 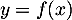 et
et 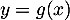 et donc en particulier
et donc en particulier
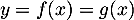 , c'est-à-dire avec les expressions précédentes,
, c'est-à-dire avec les expressions précédentes,
![\[\begin{array}{cll}&&\dfrac{x+3}{x+2}=\dfrac{-x+1}{x+2}\\[1em]
&\iff&\dfrac{x+3}{x+2}-\dfrac{-x+1}{x+2}=\dfrac{2x+2}{x+2}=0\enar\]](/Generateur-Devoirs/2nde/Chap3/exTSinter_c/9.png)
On a donc une équation quotient nulle, avec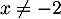 et
et 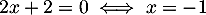 .
.
Enfin, pour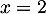 , l'ordonnée correspondante est
, l'ordonnée correspondante est
![\[y=f(-1)=g(-1)=2\]](/Generateur-Devoirs/2nde/Chap3/exTSinter_c/13.png)
Il y a donc un unique point d'intersection: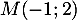
Tag:Inéquations et tableaux de signes
Voir aussi:
Quelques devoirs
sur les équations, inéquations et tableaux de signes
sur les inéquations et tableaux de signes, et statistiques: moyenne, écart type, médianne et quartile, et représentation graphique par un diagramme en boîtes (ou boîtes à moustaches)
Statistiques: calculs de la moyenne et de l'écart type d'une série pondérée. Résolution d'inéquations. Ensemble de de définition de fonctions. Exercice complet sur les fonctions: sens de variation, courbe représentative et résolution graphique d'inéquations.
pourcentage et évolutions (taux global), résolution d'inéquations (tableaux de signes), et un problème complet avec des fonctions (bénéfice d'une société, rentabilité et bénéfice maximal)
pourcentage et probabilités, et deux tableaux de signes. Intersection de deux courbes
