Jeu avec 2 dés

Exercice corrigé - maths en seconde générale

Énoncé

On lance un dé à six faces, numérotées de 1 à 6, bien équilibré. La règle du jeu est la suivante: si le chiffre obtenu est inférieur ou égal à 2, on le relance une deuxième fois et on ajoute alors le nouveau chiffre obtenu au premier; si le chiffre obtenu est supérieur ou égal à 3, on conserve ce résultat.

Le but du jeu est d'obtenir au final le plus grand nombre.

1. Représenter toutes les issues possibles à l'aide d'un arbre.
2. Combien y a-t-il d'issues élémentaires ?
3. Quel est le plus grand score que l'on peut obtenir ? Quelle est la probabilité de l'obtenir ?
4. Quelle est la probabilité d'obtenir un score supérieur ou égal à 6 ?

Correction

$\psset{unit=1cm} \begin{pspicture}(0,-3.2)(8,7) \rput(1,6.3){$1^{\mbox{\scriptsize{er}}}$ lancer} \psline[linewidth=0.6pt](0,0)(2,4)\rput(2.2,4){1} \psline[linewidth=0.6pt](0,0)(2,1)\rput(2.2,1){2} \psline[linewidth=0.6pt](0,0)(2,-1.5)\rput(2.2,-1.5){3} \psline[linewidth=0.6pt](0,0)(2,-2)\rput(2.2,-2){4} \psline[linewidth=0.6pt](0,0)(2,-2.5)\rput(2.2,-2.5){5} \psline[linewidth=0.6pt](0,0)(2,-3)\rput(2.2,-3){6} \rput(3.5,6.3){$2^{\mbox{\scriptsize{\`eme}}}$ lancer} \rput(3.5,5.8){(\'eventuel)} \psline[linewidth=0.6pt](2.4,4)(4,5)\rput(4.2,5){1} \psline[linewidth=0.6pt](2.4,4)(4,4.5)\rput(4.2,4.5){2} \psline[linewidth=0.6pt](2.4,4)(4,4)\rput(4.2,4){3} \psline[linewidth=0.6pt](2.4,4)(4,3.5)\rput(4.2,3.5){4} \psline[linewidth=0.6pt](2.4,4)(4,3)\rput(4.2,3){5} \psline[linewidth=0.6pt](2.4,4)(4,2.5)\rput(4.2,2.5){6} \psline[linewidth=0.6pt](2.4,1)(4,2)\rput(4.2,2){1} \psline[linewidth=0.6pt](2.4,1)(4,1.5)\rput(4.2,1.5){2} \psline[linewidth=0.6pt](2.4,1)(4,1)\rput(4.2,1){3} \psline[linewidth=0.6pt](2.4,1)(4,.5)\rput(4.2,.5){4} \psline[linewidth=0.6pt](2.4,1)(4,0)\rput(4.2,0){5} \psline[linewidth=0.6pt](2.4,1)(4,-.5)\rput(4.2,-.5){6} \rput(6.,6.3){R\'esultat} \psline[linewidth=0.6pt]{->}(4.4,5.0)(6,5.0)\rput(6.2,5.0){2} \psline[linewidth=0.6pt]{->}(4.4,4.5)(6,4.5)\rput(6.2,4.5){3} \psline[linewidth=0.6pt]{->}(4.4,4.0)(6,4.0)\rput(6.2,4.0){4} \psline[linewidth=0.6pt]{->}(4.4,3.5)(6,3.5)\rput(6.2,3.5){5} \psline[linewidth=0.6pt]{->}(4.4,3.0)(6,3.0)\rput(6.2,3.0){6} \psline[linewidth=0.6pt]{->}(4.4,2.5)(6,2.5)\rput(6.2,2.5){7} \psline[linewidth=0.6pt]{->}(4.4,2.0)(6,2.0)\rput(6.2,2.0){3} \psline[linewidth=0.6pt]{->}(4.4,1.5)(6,1.5)\rput(6.2,1.5){4} \psline[linewidth=0.6pt]{->}(4.4,1.0)(6,1.0)\rput(6.2,1.0){5} \psline[linewidth=0.6pt]{->}(4.4,0.5)(6,0.5)\rput(6.2,0.5){6} \psline[linewidth=0.6pt]{->}(4.4,0.0)(6,0.0)\rput(6.2,0.0){7} \psline[linewidth=0.6pt]{->}(4.4,-0.5)(6,-0.5)\rput(6.2,-0.5){8} \psline[linewidth=0.6pt]{->}(2.4,-1.5)(6,-1.5)\rput(6.2,-1.5){3} \psline[linewidth=0.6pt]{->}(2.4,-2.0)(6,-2.0)\rput(6.2,-2.0){4} \psline[linewidth=0.6pt]{->}(2.4,-2.5)(6,-2.5)\rput(6.2,-2.5){5} \psline[linewidth=0.6pt]{->}(2.4,-3.0)(6,-3.0)\rput(6.2,-3.0){6} \end{pspicture}$

[2.] Il y a 16 issues élémentaires possibles.
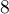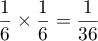[3.] Le plus grand nombre que l'on peut obtenir est . Il n'y a qu'une seule façon de l'obtenir, avec une probabilité de $$\dfrac{1}{6}\times\dfrac{1}{6}= \dfrac{1}{36}$ .
[4.] Obtenir un chiffre supérieur ou égal à 6 signifie ici obtenir un 6, un 7, ou un 8.
Il y a 5 tirages avec deux dés qui permettent d'obtenir un tel score, et un tirage avec un seul dé (tirer le 6 justement).
La probabilité probabilité d'obtenir un chiffre supérieur ou égal à 6 est donc:
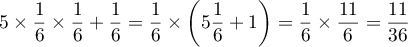
$$5\tm\dfrac{1}{6}\tm\dfrac{1}{6}+\dfrac{1}{6} =\dfrac{1}{6}\times\left( 5\dfrac16+1\right) =\dfrac16\times\dfrac{11}{6} =\dfrac{11}{36}$

Tag:Probabilités

Autres sujets au hasard:

Voir aussi: