Théorème de Rolle - Énoncé et démonstration
Colle de mathématiques
Sujet de colle de maths:- DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)
- Rolle - AFThéorème de Rolle et théorème des accroissements finis
Énoncé du sujet
Énoncer et démontrer le théorème de Rolle.
Correction
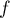 une fonction continue sur
une fonction continue sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exR0_c/2.png) et dérivable sur
et dérivable sur ![$]a;b[$](/Generateur-Devoirs/Colles/Calcul/exR0_c/3.png) , et telle que
, et telle que 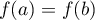 ,
alors il existe
,
alors il existe ![$c\in]a;b[$](/Generateur-Devoirs/Colles/Calcul/exR0_c/5.png) tel que
tel que
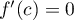 .
.
(.8,1.6)(2,3.5)(3,1)(4,1)(5,1.5)
\psline{<->}(1,3.51)(3,3.51)
\psline{<->}(2.3,.88)(4.7,.88)
\psline[linestyle=dashed](.5,0)(.5,1.5)(0,1.5)(5,1.5)(5,0)
\rput[r](-.2,1.5){$f(a)=f(b)$}
\rput(.5,-.3){$a$}
\rput(5,-.3){$b$}
\end{pspicture}\]](/Generateur-Devoirs/Colles/Calcul/exR0_c/7.png)
Démonstration:
La démonstration peut être vue comme une conséquence de la propriété des fonctions continues: si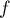 est continue sur
est continue sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exR0_c/9.png) , alors
, alors 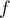 est bornée et atteint ses bornes.
Par exemple en
est bornée et atteint ses bornes.
Par exemple en 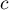
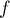 atteint un maximum ou un minimum et donc
atteint un maximum ou un minimum et donc
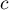 est un point critique c'est-à-dire
est un point critique c'est-à-dire 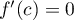 .
.
Le seul point qui reste à vérifie est que![$c\in]a;b[$](/Generateur-Devoirs/Colles/Calcul/exR0_c/15.png) ,
c'est-à-dire que
,
c'est-à-dire que 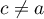 et
et 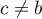 .
Ceci est en effet le cas lorsque
.
Ceci est en effet le cas lorsque 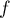 n'est pas constante.
n'est pas constante.
Plus précisément, si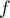 est constante sur
est constante sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exR0_c/20.png) ,
alors pour tout
,
alors pour tout ![$x\in[a;b]$](/Generateur-Devoirs/Colles/Calcul/exR0_c/21.png) ,
on a
,
on a 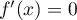 , et le théorème est clairement vérifié.
, et le théorème est clairement vérifié.
Sinon, comme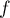 est continue sur
est continue sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exR0_c/24.png) ,
, 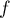 y est bornée,
et on pose
y est bornée,
et on pose ![$m=\dsp\inf_{x\in[a;b]} f(x)$](/Generateur-Devoirs/Colles/Calcul/exR0_c/26.png) et
et ![$M=\dsp\sup_{x\in[a;b]}f(x)$](/Generateur-Devoirs/Colles/Calcul/exR0_c/27.png) .
Comme
.
Comme 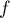 n'est pas constante, on a
n'est pas constante, on a 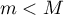 , et soit
, et soit
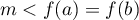 soit
soit 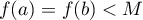 .
.
Dans le premier cas par exemple, il existe donc![$c\in]a;b[$](/Generateur-Devoirs/Colles/Calcul/exR0_c/32.png) tel que
tel que
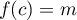 et en ce point critique
et en ce point critique 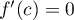 .
.
Le raisonnement est analogue dans le deuxième cas.
Correction
Théorème: Soit(.8,1.6)(2,3.5)(3,1)(4,1)(5,1.5)
\psline{<->}(1,3.51)(3,3.51)
\psline{<->}(2.3,.88)(4.7,.88)
\psline[linestyle=dashed](.5,0)(.5,1.5)(0,1.5)(5,1.5)(5,0)
\rput[r](-.2,1.5){$f(a)=f(b)$}
\rput(.5,-.3){$a$}
\rput(5,-.3){$b$}
\end{pspicture}\]](/Generateur-Devoirs/Colles/Calcul/exR0_c/7.png)
Démonstration:
La démonstration peut être vue comme une conséquence de la propriété des fonctions continues: si
Le seul point qui reste à vérifie est que
Plus précisément, si
Sinon, comme
Dans le premier cas par exemple, il existe donc
Le raisonnement est analogue dans le deuxième cas.
Tags:DérivéeRolle - AF
Autres sujets au hasard:
