Tangente commune à une parabole et une hyperbole
Colle de mathématiques
Sujet de colle de maths:- DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)
Énoncé du sujet
Montrer que les courbes d'équations 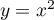 et
et 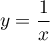 admettent une tangente commune.
admettent une tangente commune.
Correction
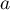 de la courbe d'équation
de la courbe d'équation 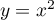 a pour équation
a pour équation
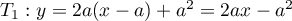 ,
et celle en
,
et celle en 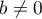 de la courbe d'équation
de la courbe d'équation 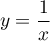 a pour équation
a pour équation
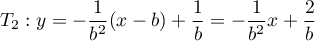 .
.
Pour qu'une tangente soit commune, il faut et suffit donc que
![\[\la\begin{array}{l}
2a=-\dfrac{1}{b^2}\\[.8em]
-a^2=\dfrac2b\enar\right.
\iff
\la\begin{array}{l}
a=-\dfrac{1}{2b^2}\\[.8em]
-\dfrac{1}{4b^4}=\dfrac2b
\iff-b=8b^4
\iff 8b^4+b=b(8b^3+1)=0
\enar\right.
\]](/Generateur-Devoirs/Colles/Calcul/extg2_c/7.png)
On trouve ainsi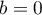 , ce qui est impossible,
ou
, ce qui est impossible,
ou  et donc
et donc 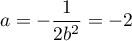 .
.
Correction
La tangente enPour qu'une tangente soit commune, il faut et suffit donc que
![\[\la\begin{array}{l}
2a=-\dfrac{1}{b^2}\\[.8em]
-a^2=\dfrac2b\enar\right.
\iff
\la\begin{array}{l}
a=-\dfrac{1}{2b^2}\\[.8em]
-\dfrac{1}{4b^4}=\dfrac2b
\iff-b=8b^4
\iff 8b^4+b=b(8b^3+1)=0
\enar\right.
\]](/Generateur-Devoirs/Colles/Calcul/extg2_c/7.png)
On trouve ainsi
Tag:Dérivée
Autres sujets au hasard:

Voir aussi: