Tangente à un cercle passant par un point et calcul de distance
Colle de mathématiques
Sujet de colle de maths:- Géométrie plane cartésienneGéométrie plane cartésienne, géométrie et coordonnées dans le plan
Énoncé du sujet
On considère, dans un repère orthonormal du plan,
le point 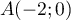 et le cercle
et le cercle 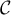 de centre
de centre 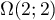 et de rayon
et de rayon 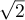 .
.
On note une droite passant par
une droite passant par 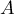 et tangente
à
et tangente
à 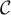 en
en  .
.
Déterminer les coordonnées du point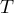 et la distance
et la distance  .
.
On note
Déterminer les coordonnées du point
Correction
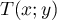 .
.
Comme la droite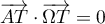 est tangente au cercle, elle est en particulier perpendiculaire au rayon, soit
est tangente au cercle, elle est en particulier perpendiculaire au rayon, soit 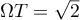 .
.
De plus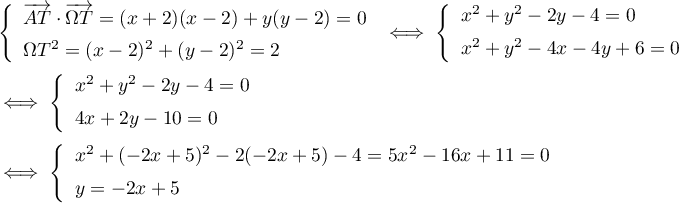 est aussi un point du cercle, et donc
est aussi un point du cercle, et donc  .
.
Ces deux relations s'écrivent soit
![\[\la\begin{array}{l}
\overrightarrow{AT}\cdot\overrightarrow{\Omega T}=(x+2)(x-2)+y(y-2)=0\\[.5em]
\Omega T^2=(x-2)^2+(y-2)^2=2
\enar\right.\]](/Generateur-Devoirs/Colles/Geom2D/ex6_c/6.png)
soit, en développant et ordonnant
![\[\la\begin{array}{l}
x^2+y^2-2y-4=0\\[.5em]
x^2+y^2-4x-4y+6=0
\enar\right.\]](/Generateur-Devoirs/Colles/Geom2D/ex6_c/7.png)
En soustrayant la deuxième équation à la première, tous les termes au carré se simplifient, et on obtient le système équivalent
![\[\la\begin{array}{l}
x^2+y^2-2y-4=0\\[.5em]
4x+2y-10=0
\enar\right.\]](/Generateur-Devoirs/Colles/Geom2D/ex6_c/8.png)
On peut alors exprimer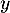 dans la deuxième équation
dans la deuxième équation
![\[\la\begin{array}{l}
x^2+y^2-2y-4=0\\[.5em]
y=-2x+5
\enar\right.\]](/Generateur-Devoirs/Colles/Geom2D/ex6_c/10.png)
puis le substituer dans la première équation
![\[\la\begin{array}{l}
x^2+(-2x+5)^2-2(-2x+5)-4=0\\[.5em]
y=-2x+5
\enar\right.\]](/Generateur-Devoirs/Colles/Geom2D/ex6_c/11.png)
Cette première équation est donc une équation du second degré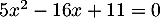 qui admet
qui admet
 comme racine évidente; la 2ème racine étant alors
comme racine évidente; la 2ème racine étant alors 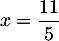 .
(ou on peut calculer le discriminat
.
(ou on peut calculer le discriminat  , puis les racines ...)
, puis les racines ...)
On calcule alors les ordonnées correspondantes grâce à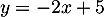 .
.
On trouve donc finalement deux possibilités pour le point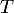 :
:
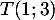 et
et 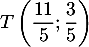 .
.
Correction
SoitComme la droite
De plus
Ces deux relations s'écrivent soit
![\[\la\begin{array}{l}
\overrightarrow{AT}\cdot\overrightarrow{\Omega T}=(x+2)(x-2)+y(y-2)=0\\[.5em]
\Omega T^2=(x-2)^2+(y-2)^2=2
\enar\right.\]](/Generateur-Devoirs/Colles/Geom2D/ex6_c/6.png)
soit, en développant et ordonnant
![\[\la\begin{array}{l}
x^2+y^2-2y-4=0\\[.5em]
x^2+y^2-4x-4y+6=0
\enar\right.\]](/Generateur-Devoirs/Colles/Geom2D/ex6_c/7.png)
En soustrayant la deuxième équation à la première, tous les termes au carré se simplifient, et on obtient le système équivalent
![\[\la\begin{array}{l}
x^2+y^2-2y-4=0\\[.5em]
4x+2y-10=0
\enar\right.\]](/Generateur-Devoirs/Colles/Geom2D/ex6_c/8.png)
On peut alors exprimer
![\[\la\begin{array}{l}
x^2+y^2-2y-4=0\\[.5em]
y=-2x+5
\enar\right.\]](/Generateur-Devoirs/Colles/Geom2D/ex6_c/10.png)
puis le substituer dans la première équation
![\[\la\begin{array}{l}
x^2+(-2x+5)^2-2(-2x+5)-4=0\\[.5em]
y=-2x+5
\enar\right.\]](/Generateur-Devoirs/Colles/Geom2D/ex6_c/11.png)
Cette première équation est donc une équation du second degré
On calcule alors les ordonnées correspondantes grâce à
On trouve donc finalement deux possibilités pour le point
Tag:Géométrie plane cartésienne
Autres sujets au hasard:

Voir aussi: