Suite récurrente et série (bis)
Colle de mathématiques
Sujet de colle de maths:- SériesSéries
Énoncé du sujet
On pose 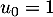 . Pour tout
. Pour tout 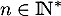 , on note
, on note
![\[u_{n+1}=u_n+u_n^2\]](/Generateur-Devoirs/Colles/Series/srs2/3.png)
- Montrer que la suite
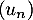 diverge vers
diverge vers 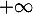 .
.
- On pose
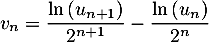 .
.
Montrer que la série de terme général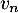 converge.
converge.
- On pose
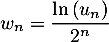 .
.
Montrer que la suite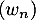 converge, on note
converge, on note 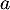 sa limite.
sa limite.
- Montrer que
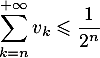 .
.
- Montrer que
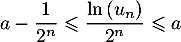 .
.
Correction
Correction
Oral ENSAE - Saclay - 2019- On montre par récurrence que la suite
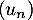 est strictement positive.
est strictement positive.
En effet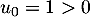 puis, si
puis, si 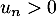 alors
alors 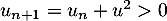 .
.
On a donc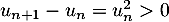 et cette suite est donc strictement croissante.
Elle converge donc vers une limite
et cette suite est donc strictement croissante.
Elle converge donc vers une limite 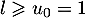 ou diverge vers
ou diverge vers 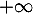 .
.
Mais si elle converge vers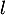 , alors par passage à la limite dans la relation de récurrence, on a nécessairement
, alors par passage à la limite dans la relation de récurrence, on a nécessairement
![\[l=l+l^2\iff l=0\]](/Generateur-Devoirs/Colles/Series/srs2_c/9.png)
ce qui est impossible car on a vu que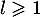 .
.
Ainsi, la suite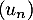 diverge vers
diverge vers 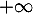 .
.
- On a
![\[\begin{array}{lcl}\ln\left( u_{n+1}\rp&=&\ln\left( u_n+u_n^2\rp\\[.5em]
&=&\ln\left( u_n^2\left(1+\dfrac1{u_n}\rp\rp\\[1em]
&=&2\ln\left( u_n\rp+\ln\left(1+\dfrac1{u_n}\rp
\enar\]](/Generateur-Devoirs/Colles/Series/srs2_c/13.png)
et donc
![\[v_n=\dfrac1{2^{n+1}}\ln\lp1+\dfrac1{u_n}\rp\]](/Generateur-Devoirs/Colles/Series/srs2_c/14.png)
Or on a vu que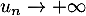 , donc
, donc 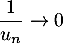 et alors
et alors
![\[v_n\underset{+\infty}{\sim}\dfrac1{2^{n+1}}\,\dfrac1{u_n}\leqslant\dfrac1{2^{n+1}}\]](/Generateur-Devoirs/Colles/Series/srs2_c/17.png)
car on a vu aussi que la suite est croissante donc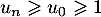 ,
donc
,
donc 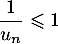 .
.
On sait de plus que la série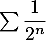 converge, comme une série géométrique de raison
converge, comme une série géométrique de raison 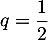 ,
et donc, par comparaison entre séries à termes positifs,
,
et donc, par comparaison entre séries à termes positifs, 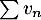 converge aussi.
converge aussi.
- On a
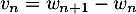 et donc la somme téléscopique
et donc la somme téléscopique
![\[\sum_{k=0}^n v_k= w_{n+1}-w_0\]](/Generateur-Devoirs/Colles/Series/srs2_c/24.png)
et donc, puisque la série de gauche converge, il en est de même de la suite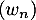 .
.
- On a vu que
![\[v_n=\dfrac1{2^{n+1}}\ln\lp1+\dfrac1{u_n}\right)
\leqslant\dfrac1{2^{n+1}}\ln(2)\]](/Generateur-Devoirs/Colles/Series/srs2_c/26.png)
car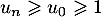 ,
donc
,
donc 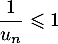 , et que la fonction ln est croissante.
, et que la fonction ln est croissante.
On a donc
![\[\sum_{k=n}^N\dfrac1{v_k}
\leqslant \ln(2)\sum_{k=n}^N\dfrac1{2^{k+1}}\]](/Generateur-Devoirs/Colles/Series/srs2_c/29.png)
avec
![\[\sum_{k=n}^N\dfrac1{2^{k+1}}
=\dfrac1{2^{n+1}}\dfrac{1-\dfrac1{2^{N-n+1}}}{1-\dfrac12}
\]](/Generateur-Devoirs/Colles/Series/srs2_c/30.png)
d'où
![\[\sum_{k=n}^{+\infty}\dfrac1{2^{k+1}}
=\dfrac1{2^n}\]](/Generateur-Devoirs/Colles/Series/srs2_c/31.png)
On a donc trouvé que
![\[\sum_{k=n}^{+\infty}v_k\leqslant\ln(2)\dfrac1{2^n}\]](/Generateur-Devoirs/Colles/Series/srs2_c/32.png)
et qui nous donne l'inégalité souhaité puisque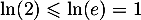 , d'où
, d'où
![\[\sum_{k=n}^{+\infty}v_k\leqslant\dfrac1{2^n}\]](/Generateur-Devoirs/Colles/Series/srs2_c/34.png)
- On a
![\[\begin{array}{lcl}\dsp\sum_{k=0}^{n-1}v_k
&=&w_n-w_0\\
&=&\dfrac{\ln(u_n)}{2^{n}}-\dfrac{\ln(u_0)}{2^0}\\[.7em]
&=&\dfrac{\ln(u_n)}{2^{n}}
\enar\]](/Generateur-Devoirs/Colles/Series/srs2_c/35.png)
car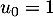 .
.
Par ailleurs
![\[\dsp\sum_{k=0}^{n-1}v_k=\sum_{k=0}^{+\infty}v_k-\sum_{k=n}^{+\infty}v_k
=a-\sum_{k=n}^{+\infty}v_k
\]](/Generateur-Devoirs/Colles/Series/srs2_c/37.png)
d'où l'encadrement souhaité avec l'inégalité de la question précédente;
Tag:Séries
Autres sujets au hasard:

Voir aussi: