Sous-espace vectoriel de polynômes et espace supplémentaire
Colle de mathématiques
Sujet de colle de maths:- Espace vectorielEspaces vectoriels
Énoncé du sujet
Dans ![$\R_2[X]$](/Generateur-Devoirs/Colles/ev/exssevpol/1.png) , l'ensemble des polynômes de degré inférieur ou égal à 2, on considère l'ensemble
, l'ensemble des polynômes de degré inférieur ou égal à 2, on considère l'ensemble
![\[E=\left\{ P\in\R_2[X]; P(0)=P(2)=0\right\}\]](/Generateur-Devoirs/Colles/ev/exssevpol/2.png)
- Montrer que
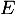 est un espace vectoriel. Quelle est sa dimension ? En donner une base.
est un espace vectoriel. Quelle est sa dimension ? En donner une base.
- Donner un espace supplémentaire de
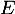 .
.
Correction
Correction
- On montre que
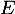 est un sous-espace vectoriel de
est un sous-espace vectoriel de ![$\R_2[X]$](/Generateur-Devoirs/Colles/ev/exssevpol_c/2.png) .
Tout d'abord le polynôme nul appartient bien à
.
Tout d'abord le polynôme nul appartient bien à 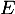 .
.
Ensuite, pour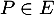 et
et 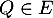 , c'est-à-dire
, c'est-à-dire 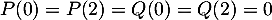 alors le polynôme
alors le polynôme 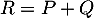 vérifie aussi
vérifie aussi
![\[R(0)=(P+Q)(0)=P(0)+Q(0)=0\]](/Generateur-Devoirs/Colles/ev/exssevpol_c/8.png)
et de même .
.
En multipliant par un réel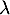 quelconque on arrive au même résultat: si
quelconque on arrive au même résultat: si 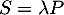 , alors
, alors 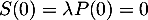 et de aussi
et de aussi 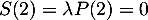 .
.
On vient donc de montrer que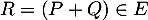 et
et 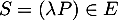 , c'est-à-dire que
, c'est-à-dire que 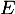 est stable par combinaison linéaire, ce qui montre que
est stable par combinaison linéaire, ce qui montre que 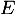 est un sous-espace vectoriel de
est un sous-espace vectoriel de ![$\R_2[X]$](/Generateur-Devoirs/Colles/ev/exssevpol_c/18.png) et a en particulier la structure d'un espace vectoriel.
et a en particulier la structure d'un espace vectoriel.
Les polynômes de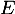 admettent 0 et 2 comme racines. Ils se factorisent donc par
admettent 0 et 2 comme racines. Ils se factorisent donc par 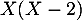 .
Ainsi,
.
Ainsi,
![\[E=\text{Vect}\left\{ X(X-2)\right\}\]](/Generateur-Devoirs/Colles/ev/exssevpol_c/21.png)
En particulier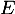 est de dimension 1, et une base est formée de un vecteur: le polynôme précédent.
est de dimension 1, et une base est formée de un vecteur: le polynôme précédent.
- On peut définir un supplémentaire
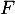 par une base.
par une base.
D'après le théorème de la base incomplète, on peut compléter le polynôme précédent par deux autres pris dans la base canonique de![$\R_2[X]$](/Generateur-Devoirs/Colles/ev/exssevpol_c/24.png) pour obtenir une base de
pour obtenir une base de ![$E_2[X]$](/Generateur-Devoirs/Colles/ev/exssevpol_c/25.png) .
Ces deux polynômes formeront alors une base d'un supplémentaire de
.
Ces deux polynômes formeront alors une base d'un supplémentaire de 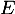 .
.
Par exemple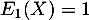 et
et ![$E_2[X]=X$](/Generateur-Devoirs/Colles/ev/exssevpol_c/28.png) , et le sous-espace vectoriel
, et le sous-espace vectoriel
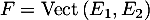 .
.
Il reste à vérifier que le choix de ces deux polynômes dans la base canonique convient, à savoir que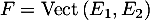 .
.
Soit un polynôme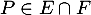 , alors
, alors
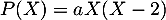 car
car 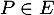 et
et 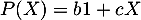 car
car 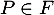 .
.
On doit donc avoir, pour tout réel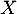 ,
, 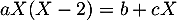 .
.
En prenant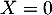 , on obtient
, on obtient 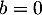 , et avec
, et avec 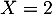 , on obtient ensuite
, on obtient ensuite 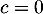 .
Enfin, comme on a obtenu jusque là que
.
Enfin, comme on a obtenu jusque là que 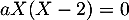 pour tout réel
pour tout réel 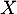 , le choix n'importe quel autre réel, que 0 et 2, donne maintenant
, le choix n'importe quel autre réel, que 0 et 2, donne maintenant  .
.
On a donc trouvé que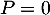 est le polynôme nul, c'est-à-dire
est le polynôme nul, c'est-à-dire 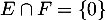 .
.
Ces deux sous espaces sont donc en somme directe, et avec un argument de dimensions: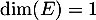 et
et 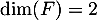 , on en déduit qu'ils sont en somme directe dans
, on en déduit qu'ils sont en somme directe dans ![$\R_2[X]$](/Generateur-Devoirs/Colles/ev/exssevpol_c/49.png) puisque
puisque ![$\dim\left( \R_2[X]\rp=3$](/Generateur-Devoirs/Colles/ev/exssevpol_c/50.png) , c'est-à-dire qu'ils sont supplémentaires.
, c'est-à-dire qu'ils sont supplémentaires.
Tag:Espace vectoriel
Autres sujets au hasard:

Voir aussi: