Rayon de convergence


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

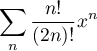
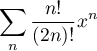
Déterminer le rayon de convergence de la série entière $\dsp\sum_n\frac{n!}{(2n)!}x^n$


Correction

Correction

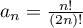Soit $a_n=\frac{n!}{(2n)!}$. Alors
\[\frac{a_{n+1}}{a_n}=\frac{n+1}{(2n+2)(2n+1)}=\frac{1}{4n+2}\to 0\]

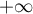D'après la règle de d'Alembert, le rayon de convergence est $+\infty$.


Tag:Séries entières

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0