Rayon de convergence
Colle de mathématiques
Sujet de colle de maths:- Séries entièresSéries entières
Énoncé du sujet
Étudier la convergence de la série
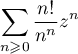 .
.
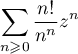 .
.
Correction
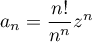 ,
alors
,
alors
![\[\dfrac{a_{n+1}}{a_n}=
\dfrac{(n+1)!\,z^{n1}}{(n+1)^{n+1}}
\tm\dfrac{n^n}{n!\,z^n}
=z\lp\dfrac{n}{n+1}\rp^n
=ze^{n\ln\lp\dfrac{n}{n+1}\right)}
=ze^{-n\ln\lp1+\dfrac1n\right)}\]](/Generateur-Devoirs/Colles/SeriesEnt/exRC14_c/2.png)
Or, pour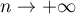 ,
, 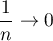 , et, au 1er ordre,
, et, au 1er ordre,
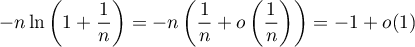 .
.
Ainsi,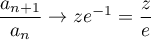 et la série est convergente pour
et la série est convergente pour 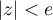 .
.
En d'autres termes, le rayon de convergence de cette série entière est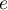 .
.
Correction
Soit![\[\dfrac{a_{n+1}}{a_n}=
\dfrac{(n+1)!\,z^{n1}}{(n+1)^{n+1}}
\tm\dfrac{n^n}{n!\,z^n}
=z\lp\dfrac{n}{n+1}\rp^n
=ze^{n\ln\lp\dfrac{n}{n+1}\right)}
=ze^{-n\ln\lp1+\dfrac1n\right)}\]](/Generateur-Devoirs/Colles/SeriesEnt/exRC14_c/2.png)
Or, pour
Ainsi,
En d'autres termes, le rayon de convergence de cette série entière est
Tag:Séries entières
Autres sujets au hasard:

Voir aussi: