Propriété de l'intégrale d'une fonction avec une symétrie


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

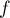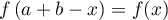Soit $f$ une fonction continue sur $[a;b]$ à valeurs réelles telle que, pour tout $x\in[a;b]$, $f\left( a+b-x\rp=f(x)$.
Montrer que $\dsp\int_a^b xf(x)\,dx=\dfrac{a+b}{2}\int_a^bf(x)\,dx$.


Correction

Correction

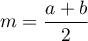Soit $m=\dfrac{a+b}{2}$, alors la propriété donnée sur 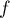$f$ exprime que sa courbe est symétrique par rapport à la droite d'équation $x=m$. En effet, si on pose $u=m-x$, alors
\[\begin{array}{ll}f(m-x)&=f\lp\dfrac{a+b}{2}-x\rp\\ &=f\Bigl( a+b-\left( x+\dfrac{a+b}{2}\rp\Bigr) \\ &=f\left( x+\dfrac{a+b}{2}\rp\Bigr) \\ &=f(m+x)\enar\]



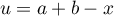En ayant remarqué ou non cette symétrie graphique, la propriété donnée sur $f$ nous incite fortement à utiliser le changement de variable $u=a+b-x$ dans l'intégrale.
On alors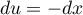 $du=-dx$ et, en n'oubliant pas les bornes,
\[I=\int_a^b xf(x)\,dx=-\int_b^a (a+b-u)f\left( a+b-u\rp\,du\]

soit, avec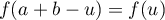 $f(a+b-u)=f(u)$ et en séparant l'intégrale en deux:
\[\begin{array}{ll}I&\dsp=(a+b)\int_a^b f(u)du-\int_a^b uf(u)du\\[1em] &\dsp=(a+b)\int_a^bf(u)du-I\enar\right.\]

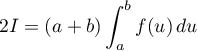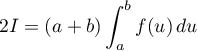On trouve donc $2I=(a+b)\dsp\int_a^bf(u)\,du$ d'où le résultat.


Tag:Intégrale

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0