Calculer l'intégrale …
Colle de mathématiques
Sujet de colle de maths:- IntégraleIntégrale
Énoncé du sujet
Calculer 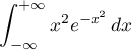 sachant que
sachant que 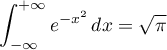
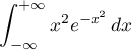 sachant que
sachant que 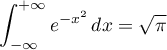
Correction
![\[\int_{-\infty}^{+\infty}x^2e^{-x^2}\,dx
=\int_{-\infty}^{+\infty}x \left( xe^{-x^2}\right) dx
=\left[ x\dfrac{e^{-x^2}}{-2}\rb_{-\infty}^{+\infty}
-\int_{-\infty}^{+\infty}\dfrac{e^{-x^2}}{-2}\,dx
=\dfrac12\sqrt\pi
\]](/Generateur-Devoirs/Colles/Integrale/exC7_c/1.png)
car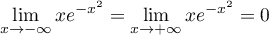 .
.
Correction
En intégrant par parties,![\[\int_{-\infty}^{+\infty}x^2e^{-x^2}\,dx
=\int_{-\infty}^{+\infty}x \left( xe^{-x^2}\right) dx
=\left[ x\dfrac{e^{-x^2}}{-2}\rb_{-\infty}^{+\infty}
-\int_{-\infty}^{+\infty}\dfrac{e^{-x^2}}{-2}\,dx
=\dfrac12\sqrt\pi
\]](/Generateur-Devoirs/Colles/Integrale/exC7_c/1.png)
car
Tag:Intégrale
Autres sujets au hasard:

Voir aussi: