Probabilités avec une densité
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Soit la fonction
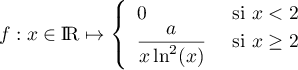
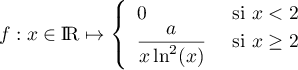
- Déterminer
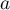 pour cette fonction soit la densité de probabilité
d'une variable aléatoire
pour cette fonction soit la densité de probabilité
d'une variable aléatoire 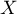 .
.
- Déterminer la fonction de répartition de
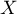 .
.
- Calculer les probabilités
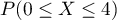 et
et 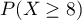 .
.
Correction
Correction
-
-
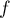 est continue et dérivable sur
est continue et dérivable sur 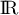 ,
sauf en un nombre fini de points, ici sauf en 2.
,
sauf en un nombre fini de points, ici sauf en 2.
-
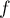 est positive sur
est positive sur 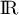 .
.
- Il reste à montrer que
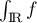 converge et vaut 1.
converge et vaut 1.
On a
![\[\int_{-\infty}^{+\infty}f(x)dx=\int_2^{+\infty}\dfrac{a}{x\ln^2(x)}dx\]](/Generateur-Devoirs/Colles/VAC/prbds_c/6.png)
avec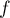 continue sur
continue sur 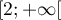 et donc il suffit d'étudier
la convergence de l'intégrale généralisée en
et donc il suffit d'étudier
la convergence de l'intégrale généralisée en 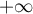 .
On connaît une primitive de cette fonction
.
On connaît une primitive de cette fonction
![\[\int_2^A\dfrac1{x\ln^2(x)}dx=
\lb-\dfrac1{\ln(x)}\rb_2^A
=-\dfrac1{\ln(A)}+\dfrac1{\ln(2)}\]](/Generateur-Devoirs/Colles/VAC/prbds_c/10.png)
et donc l'intégrale est convergente avec
![\[\int_2^{+\infty}\dfrac{a}{x\ln^2(x)}dx=\dfrac{a}{\ln(2)}\]](/Generateur-Devoirs/Colles/VAC/prbds_c/11.png)
et on doit donc avoir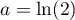 pour que la valeur de cette intégrale
soit 1.
pour que la valeur de cette intégrale
soit 1.
-
- Le calcul précédent donne aussi la fonction de répartition.
Pour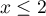 , on a
, on a 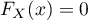 , et pour
, et pour 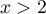 ,
,
![\[\begin{array}{ll}F_X(x)&=P(X\leq x)\\[.6em]
&=\dsp\int_{-\infty}^x f(x)dx\\
&=\dsp\ln(2)\int_2^x\dfrac1{x\ln^2(x)}dx\\[1.2em]
&=\ln(2)\lb-\dfrac1{\ln(x)}\rb_2^x\\[1em]
&=-\dfrac{\ln(2)}{\ln(x)}+1\enar\]](/Generateur-Devoirs/Colles/VAC/prbds_c/16.png)
- En utilisant la fonction de répartition, on a
![\[P(0\leq X\leq2)=F_X(2)-F_X(0)=
1-\dfrac{\ln(2)}{\ln(4)}\]](/Generateur-Devoirs/Colles/VAC/prbds_c/17.png)
soit, avec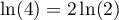 ,
,
![\[P(0\leq X\leq2)=\dfrac12\]](/Generateur-Devoirs/Colles/VAC/prbds_c/19.png)
De même,
![\[P(X\geq8)=1-F_X(8)=\dfrac{\ln(2)}{\ln(8)}=\dfrac13\]](/Generateur-Devoirs/Colles/VAC/prbds_c/20.png)
Tag:Variables aléatoires continues
Autres sujets au hasard:
