Nombre de racines d'un polynôme (suivant la parité de son degré)
Colle de mathématiques
Sujet de colle de maths:- Rolle - AFThéorème de Rolle et théorème des accroissements finis
- PolynômePolynômes
Énoncé du sujet
Soit, pour un entier  ,
le polynôme
,
le polynôme  .
.
Montrer que si est pair
est pair 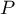 admet au plus quatre racines réelles
distinctes, tandis que si
admet au plus quatre racines réelles
distinctes, tandis que si  est impaire
est impaire  admet au plus trois racines
réelles distinctes.
admet au plus trois racines
réelles distinctes.
Montrer que si
Correction
![\[P'(x)=2(n+2)x^{n+1}-2(n+2)x=2(n+2)x\left( x^n-1\rp\]](/Generateur-Devoirs/Colles/Calcul/exR3_c/1.png)
Correction
On a- Si
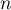 est pair, l'équation
est pair, l'équation  admet deux racines réelles,
admet deux racines réelles,
 et
et  , et donc
, et donc 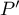 admet exactement trois racines réelles:
admet exactement trois racines réelles:
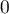 ,
,  et
et 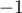 .
.
Si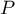 admettait plus de quatre récines réelles distinctes,
donc au moins cinq:
admettait plus de quatre récines réelles distinctes,
donc au moins cinq:
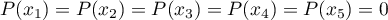 , alors d'après le théorème
de Rolle appliqué quatre fois sur chaque intervalle
, alors d'après le théorème
de Rolle appliqué quatre fois sur chaque intervalle ![$[x_i;x_{i+1}]$](/Generateur-Devoirs/Colles/Calcul/exR3_c/12.png) ,
,
 aurait quatre racines distinctes.
aurait quatre racines distinctes.
Or nous venons de voir que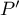 n'avait que trois racines;
c'est donc impossible, et
n'avait que trois racines;
c'est donc impossible, et 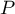 a au plus quatre racines réelles distinctes.
a au plus quatre racines réelles distinctes.
- On procède de même si
 est impair.
est impair.
Cette fois par contre l'équation n'admet qu'une seul solution,
n'admet qu'une seul solution,
 , et
, et 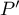 n'a donc que deux racines réelles
n'a donc que deux racines réelles 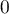 et
et  ,
et
,
et 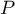 pas plus de trois racines réelles distinctes.
pas plus de trois racines réelles distinctes.
Tags:Rolle - AFPolynôme
Autres sujets au hasard:

Voir aussi: