Minimum de la norme d'une somme
Colle de mathématiques
Sujet de colle de maths:- Espaces euclidiensEspaces euclidiens, produit scalaire
Énoncé du sujet
Soit 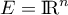 muni du produit scalaire canonique,
et
muni du produit scalaire canonique,
et 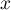 ,
, 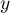 deux éléments de
deux éléments de 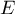 .
Montrer que
.
Montrer que 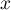 et
et 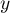 sont orthogonaux si et seulement si
sont orthogonaux si et seulement si
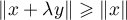 pour tout
pour tout 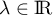 .
.
Correction
![\[\|x+\lambda y\|^2=\|x\|^2+2\lambda \langle x,y\rangle+\lambda^2\|y\|^2\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex0_c/1.png)
et donc
![\[\begin{array}{ll}\|x+\lambda y\|\geq\|x\|&\iff\|x+\lambda y\|^2\geq \|x\|^2\\[.6em]
&\iff2\lambda \langle x,y\rangle+\lambda^2\|y\|^2\geq 0\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex0_c/2.png)
Si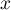 est orthogonal à
est orthogonal à 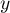 , donc
, donc 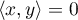 ,
alors l'inégalité précédente est bien vérifiée pour tout
,
alors l'inégalité précédente est bien vérifiée pour tout 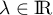 .
.
Réciproquement, si
![\[P(\lambda)=2\lambda \langle x,y\rangle+\lambda^2\|y\|^2\geq 0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex0_c/7.png)
pour tout réel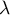 ,
alors le discriminant du polynôme du second degré
,
alors le discriminant du polynôme du second degré 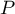 est négatif ou nul, soit
est négatif ou nul, soit
![\[\Delta=4\langle x,y\rangle^2\leq 0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex0_c/10.png)
Ceci n'est possible que si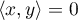 , c'est-à-dire si
, c'est-à-dire si 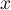 et
et 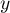 sont orthogonaux.
sont orthogonaux.
Correction
On aet donc
![\[\begin{array}{ll}\|x+\lambda y\|\geq\|x\|&\iff\|x+\lambda y\|^2\geq \|x\|^2\\[.6em]
&\iff2\lambda \langle x,y\rangle+\lambda^2\|y\|^2\geq 0\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex0_c/2.png)
Si
Réciproquement, si
pour tout réel
Ceci n'est possible que si
Tag:Espaces euclidiens
Autres sujets au hasard:

Voir aussi: