Ensemble de matrices stable par produit
Colle de mathématiques
Sujet de colle de maths:- MatricesMatrices
Énoncé du sujet
Pour 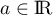 on pose
on pose
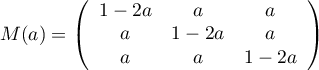 et
et 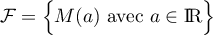 .
.
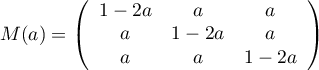 et
et - Montrer que pour tous réels
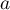 et
et  on a
on a
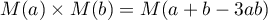 .
.
- Soit
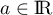 . Montrer que
. Montrer que 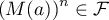 pour tout entier
pour tout entier  .
.
- Déterminer les éléments de
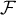 qui sont inversibles.
qui sont inversibles.
Correction
Correction
- Le produit matriciel donne le résultat
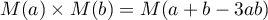 .
.
- Par récurrence:
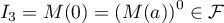 et
et 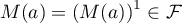 .
.
Si on suppose que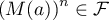 ,
c'est-à-dire que
,
c'est-à-dire que
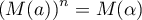 pour un certain réel
pour un certain réel  ,
alors
,
alors
![\[\begin{array}{ll}\left( M(a)\rp^{n+1}&=\left( M(a)\rp^n\times M(a)\\
&=M(\alpha)\times M(a)\\
&=M(\alpha+a)\in\mathcal{F}\enar\]](/Generateur-Devoirs/Colles/matrices/E2_c/7.png)
On vient donc de démontrer, d'après le principe de récurrence, que pour tout entier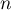 ,
,
 .
.
- Comme
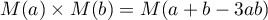 et
et  ,
pour trouver l'inverse de de
,
pour trouver l'inverse de de 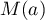 il suffit de trouver
il suffit de trouver  tel que
tel que
 , soit, si
, soit, si 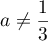 ,
, 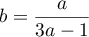 .
.
Ainsi, pour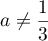 ,
, 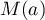 est inversible
et
est inversible
et
![\[\left( M(a)\rp^{-1}=M\left(\dfrac{a}{3a-1}\rp\]](/Generateur-Devoirs/Colles/matrices/E2_c/19.png)
Si , on a, pour tout réel
, on a, pour tout réel  ,
,
![\[M\lp\dfrac13\rp\times M(b)=M\lp\dfrac13+b-b\rp=M\lp\dfrac13\rp\]](/Generateur-Devoirs/Colles/matrices/E2_c/22.png)
ce qui montre que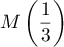 n'est pas inversible.
n'est pas inversible.
On aurait aussi pu le montrer en écrivant la matrice
![\[M\lp\dfrac13\rp=\dfrac13\lp\begin{array}{ccc}1&1&1\\1&1&1\\1&1&1\enar\rp\]](/Generateur-Devoirs/Colles/matrices/E2_c/24.png)
qui est une matrice de rang 1, donc non inversible.
Tag:Matrices
Autres sujets au hasard:

Voir aussi: