Fonction grandement simplifiable (avec fonctions trigonométriques réciproques)
Colle de mathématiques
Sujet de colle de maths:- DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)
Énoncé du sujet
Simplifier 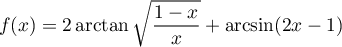
(préciser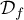 ,
,  et calculer
et calculer  ).
).
(préciser
Correction
 est définie sur
est définie sur  et
et 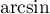 sur
sur ![$[-1;1]$](/Generateur-Devoirs/Colles/Calcul/ex4_c/4.png) et donc
et donc
 est bien définie lorsque
est bien définie lorsque
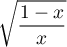 existe et
existe et
![$2x-1\in[-1;1]$](/Generateur-Devoirs/Colles/Calcul/ex4_c/7.png) .
.
 existe si et seulement si
existe si et seulement si
 et
et  .
Or
.
Or 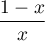 est du même signe que
est du même signe que  qui est un trinôme du second degré,
donc positif à l'intérieur de ses racines 0 et 1.
qui est un trinôme du second degré,
donc positif à l'intérieur de ses racines 0 et 1.
D'autre part,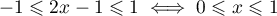 .
.
En résumé, les deux termes sont définis, donc , lorsque
, lorsque ![$x\in\mathcal{D}_f=]0;1]$](/Generateur-Devoirs/Colles/Calcul/ex4_c/15.png) .
.
Pour la dérivabilité de , on sait de plus que
, on sait de plus que 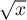 n'est pas dérivable en
n'est pas dérivable en 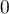 donc
donc  n'est pas dérivable en
n'est pas dérivable en 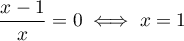 .
.
De même, n'est pas dérivable en
n'est pas dérivable en  , et ici
, et ici
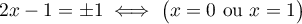 .
.
En résumé,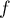 est dérivable sur
est dérivable sur ![$\mathcal{D}_{f'}=]0;1[$](/Generateur-Devoirs/Colles/Calcul/ex4_c/25.png) .
.
Pour tout![$x\in]0;1[$](/Generateur-Devoirs/Colles/Calcul/ex4_c/26.png) ,
,
![\[f'(x)=2\dfrac{u'(x)}{1+u^2(x)}+\dfrac{v'(x)}{\sqrt{1-v^2(x)}}\]](/Generateur-Devoirs/Colles/Calcul/ex4_c/27.png)
où et
et
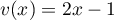 .
.
On a alors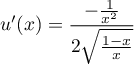 et
et 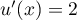 , d'où
, d'où
![\[\begin{array}{ll}f'(x)
&=-\dfrac{1}{x^2\sqrt{\frac{1-x}{x}}\lp1+\dfrac{1-x}{x}\right)}
+\dfrac2{\sqrt{1-\lp2x-1\rp^2}}\\[1em]
&=-\dfrac1{x\sqrt{\frac{1-x}{x}}}
+\dfrac2{\sqrt{4x(1-x)}}\\[1em]
&=-\dfrac1{\sqrt{x^2\frac{1-x}{x}}}
+\dfrac1{\sqrt{x(1-x)}}\\[1em]
&=0
\enar\]](/Generateur-Devoirs/Colles/Calcul/ex4_c/32.png)
Ainsi, est constante sur
est constante sur ![$]0;1]$](/Generateur-Devoirs/Colles/Calcul/ex4_c/34.png) , où elle est continue,
avec
, où elle est continue,
avec 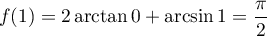 , et on a donc obtenu
, et on a donc obtenu
![\[\forall x\in]0;1]\,,\ f(x)=\dfrac\pi2\]](/Generateur-Devoirs/Colles/Calcul/ex4_c/36.png)
Correction
D'autre part,
En résumé, les deux termes sont définis, donc
Pour la dérivabilité de
De même,
En résumé,
Pour tout
![\[f'(x)=2\dfrac{u'(x)}{1+u^2(x)}+\dfrac{v'(x)}{\sqrt{1-v^2(x)}}\]](/Generateur-Devoirs/Colles/Calcul/ex4_c/27.png)
où
 et
et
On a alors
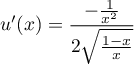 et
et ![\[\begin{array}{ll}f'(x)
&=-\dfrac{1}{x^2\sqrt{\frac{1-x}{x}}\lp1+\dfrac{1-x}{x}\right)}
+\dfrac2{\sqrt{1-\lp2x-1\rp^2}}\\[1em]
&=-\dfrac1{x\sqrt{\frac{1-x}{x}}}
+\dfrac2{\sqrt{4x(1-x)}}\\[1em]
&=-\dfrac1{\sqrt{x^2\frac{1-x}{x}}}
+\dfrac1{\sqrt{x(1-x)}}\\[1em]
&=0
\enar\]](/Generateur-Devoirs/Colles/Calcul/ex4_c/32.png)
Ainsi,
Tag:Dérivée
Autres sujets au hasard:

Voir aussi: