Fonction et sommes composées avec arctan
Colle de mathématiques
Sujet de colle de maths:- DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)
- SommesSommes des termes d'une suite
Énoncé du sujet
Montrer que, pour tout 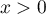 ,
,
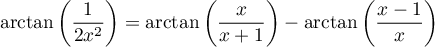 .
.
En déduire une expression de puis
puis  .
.
En déduire une expression de
 puis
puis Correction
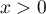 ,
,
 et
et
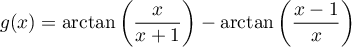 .
.
 et
et 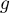 sont dérivables sur
sont dérivables sur  ,
avec
,
avec
![\[f'(x)=\dfrac{-\dfrac{1}{x^3}}{1+\lp\dfrac{1}{2x^2}\rp^2}
=-\dfrac{-4x}{4x^4+1}\]](/Generateur-Devoirs/Colles/Calcul/exarctan2_c/7.png)
et
![\[\begin{array}{ll}
g'(x)&=\dfrac{\dfrac{(x+1)-x}{(x+1)^2}}{1+\lp\dfrac{x}{x+1}\rp^2}
-\dfrac{\dfrac{x-(x-1)}{x^2}}{1+\lp\dfrac{x-1}{x}\rp^2}\\[2.8em]
&=\dfrac{1}{(x+1)^2+x^2}-\dfrac{1}{x^2+(x-1)^2}\\[1.4em]
&=\dfrac{-4x}{\lp2x^2+2x+1\rp\lp2x^2-2x+1\rp}
\enar\]](/Generateur-Devoirs/Colles/Calcul/exarctan2_c/8.png)
Or,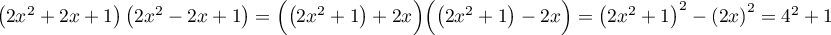 .
.
On trouve ainsi que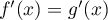 et donc
que
et donc
que 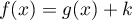 ,
, 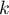 constante réelle.
constante réelle.
De plus, par exemple pour ,
, 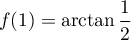 et
et 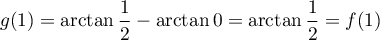 .
.
Ainsi,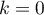 et
et 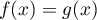 pour tout
pour tout  .
.
![\[\begin{array}{ll}
S_n&=\dsp\sum_{k=1}^n\arctan\lp\dfrac{1}{2k^2}\rp\\[1.8em]
&\dsp=\sum_{k=1}^n\arctan\lp\dfrac{k}{k+1}\right)
-\arctan\lp\dfrac{k-1}{k}\rp\\[1.8em]
&\dsp=\sum_{k=1}^n\arctan\lp\dfrac{k}{k+1}\right)
-\sum_{k=1}^n\arctan\lp\dfrac{k-1}{k}\rp\\[1.8em]
&\dsp=\sum_{k=1}^n\arctan\lp\dfrac{k}{k+1}\right)
-\sum_{k=0}^{n-1}\arctan\lp\dfrac{k}{k+1}\rp\\[1.8em]
&\dsp=\arctan\lp\dfrac{n}{n+1}\rp-\arctan0
\enar\]](/Generateur-Devoirs/Colles/Calcul/exarctan2_c/19.png)
Ainsi, pour tout entier non nul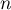 ,
,
 ,
et comme
,
et comme
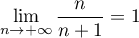 ,
on a
,
on a
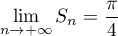 .
.
Correction
On pose, pour![\[f'(x)=\dfrac{-\dfrac{1}{x^3}}{1+\lp\dfrac{1}{2x^2}\rp^2}
=-\dfrac{-4x}{4x^4+1}\]](/Generateur-Devoirs/Colles/Calcul/exarctan2_c/7.png)
et
![\[\begin{array}{ll}
g'(x)&=\dfrac{\dfrac{(x+1)-x}{(x+1)^2}}{1+\lp\dfrac{x}{x+1}\rp^2}
-\dfrac{\dfrac{x-(x-1)}{x^2}}{1+\lp\dfrac{x-1}{x}\rp^2}\\[2.8em]
&=\dfrac{1}{(x+1)^2+x^2}-\dfrac{1}{x^2+(x-1)^2}\\[1.4em]
&=\dfrac{-4x}{\lp2x^2+2x+1\rp\lp2x^2-2x+1\rp}
\enar\]](/Generateur-Devoirs/Colles/Calcul/exarctan2_c/8.png)
Or,
On trouve ainsi que
De plus, par exemple pour
Ainsi,
![\[\begin{array}{ll}
S_n&=\dsp\sum_{k=1}^n\arctan\lp\dfrac{1}{2k^2}\rp\\[1.8em]
&\dsp=\sum_{k=1}^n\arctan\lp\dfrac{k}{k+1}\right)
-\arctan\lp\dfrac{k-1}{k}\rp\\[1.8em]
&\dsp=\sum_{k=1}^n\arctan\lp\dfrac{k}{k+1}\right)
-\sum_{k=1}^n\arctan\lp\dfrac{k-1}{k}\rp\\[1.8em]
&\dsp=\sum_{k=1}^n\arctan\lp\dfrac{k}{k+1}\right)
-\sum_{k=0}^{n-1}\arctan\lp\dfrac{k}{k+1}\rp\\[1.8em]
&\dsp=\arctan\lp\dfrac{n}{n+1}\rp-\arctan0
\enar\]](/Generateur-Devoirs/Colles/Calcul/exarctan2_c/19.png)
Ainsi, pour tout entier non nul
Tags:DérivéeSommes
Autres sujets au hasard:

Voir aussi: