🔍 Colles ☰

Famille libre de polynômes de degrés distincts

Montrer que toute famille de polynômes non nuls de degrés deux à deux distincts est libre.

Correction
On considère une famille de

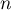polynômes

,

, … ,

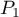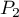de degrés respectifs

,

, … ,

.
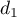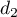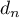Quitte à renommer ces polynômes, on peut supposer que la famille est ordonnée selon les degrés croissants: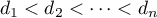 $d_1<d_2<\dots<d_n$ .

Soit maintenant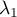 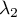$\lambda_1$ , $\lambda_2$ , … , $\lambda_n$ tels que

$\lambda_1 P_1+\lambda_2P_2+ \dots + \lambda_n P_n=0$

Cette relation se réécrit

$\lambda_nP_n=-\sum_{k=1}^{n-1}\lambda_iP_i$

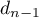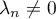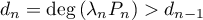Or le membre de droite de cette dernière relation est un polynôme de degré au plus $d_{n-1}$ et, si $\lambda_n\not=0$ , $d_n=\text{deg}\left( \lambda_nP_n\rp>d_{n-1}$ ce qui est impossible. On a donc necéssairement $\lambda_n=0$ .
Par une récurrence immédiate, on a alors successivement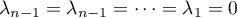 $\lambda_{n-1}=\lambda_{n-1}=\dots=\lambda_1=0$ , ce qui montre que la famille est libre.

Cacher la correction

Tags:Espace vectoriel Polynôme

Autres sujets au hasard: