Nombre de racines d'un polynôme
Colle de mathématiques
Sujet de colle de maths:- Rolle - AFThéorème de Rolle et théorème des accroissements finis
- PolynômePolynômes
Énoncé du sujet
Montrer que le polynôme 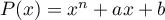 , avec
, avec  et
et  réels,
admet au plus trois racines réelles distinctes.
réels,
admet au plus trois racines réelles distinctes.
Correction
 possède
au moins quatre racines réelles distinctes:
possède
au moins quatre racines réelles distinctes:
 ,
,  ,
, 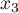 et
et 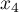 .
.
Le théorème de Rolle appliqué à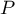 sur les intervalles
sur les intervalles
![$[x_1;x_2]$](/Generateur-Devoirs/Colles/Calcul/exR2_c/7.png) ,
, ![$[x_2;x_3]$](/Generateur-Devoirs/Colles/Calcul/exR2_c/8.png) et
et ![$[x_3;x_4]$](/Generateur-Devoirs/Colles/Calcul/exR2_c/9.png) montre que
montre que 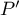 admet alors au moins
trois racines
admet alors au moins
trois racines 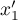 ,
, 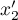 et
et 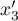 , respectivement dans les intervalles
, respectivement dans les intervalles
![$]x_1;x_2[$](/Generateur-Devoirs/Colles/Calcul/exR2_c/14.png) ,
, ![$]x_2;x_3[$](/Generateur-Devoirs/Colles/Calcul/exR2_c/15.png) et
et ![$]x_3;x_4[$](/Generateur-Devoirs/Colles/Calcul/exR2_c/16.png) .
Ces intervalles sont disjoints et ces trois racines sont distinctes aussi.
.
Ces intervalles sont disjoints et ces trois racines sont distinctes aussi.
On réitère alors le théorème de Rolle sur les deux intervalles![$[x_1';x_2']$](/Generateur-Devoirs/Colles/Calcul/exR2_c/17.png) et
et ![$[x_2';x_3']$](/Generateur-Devoirs/Colles/Calcul/exR2_c/18.png) , pour obtenir deux racines
, pour obtenir deux racines 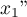 et
et 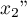 distinctes.
distinctes.
Or,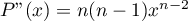 n'admet pas deux racines distinctes.
n'admet pas deux racines distinctes.
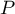 doit donc avoir au plus trois racines réelles distinctes.
doit donc avoir au plus trois racines réelles distinctes.
Correction
Supposons au contraire queLe théorème de Rolle appliqué à
On réitère alors le théorème de Rolle sur les deux intervalles
Or,
Tags:Rolle - AFPolynôme
Autres sujets au hasard:

Voir aussi: