Famille libre à compléter
Colle de mathématiques
Sujet de colle de maths:- Espace vectorielEspaces vectoriels
Énoncé du sujet
On considère dans 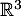 les vecteurs
les vecteurs

- Peut-on trouver un vecteur
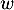 tel que
tel que 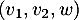 soit libre?
Si oui, construisez-en un.
soit libre?
Si oui, construisez-en un.
- Même question en remplaçant
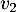 par
par 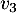 .
.
Correction
Correction
- On a
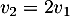 . La famille
. La famille  est donc liée.
est donc liée.
Quel que soit le vecteur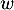 qu'on ajoute à cette famille, elle sera encore liée,
puisqu'on aura toujours
qu'on ajoute à cette famille, elle sera encore liée,
puisqu'on aura toujours 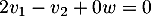 ,
combinaison linéaire dont
les coefficients ne sont pas tous nuls.
,
combinaison linéaire dont
les coefficients ne sont pas tous nuls.
- La famille
 est libre.
est libre.
D'après le théorème de la base incomplète, on sait qu'on peut utiliser, par exemple, les vecteurs de la base canonique de , qui est bien génératrice de
, qui est bien génératrice de 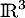 pour compléter notre famille en une base.
pour compléter notre famille en une base.
On peut essayer d'utiliser par exemple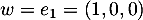 .
Il reste alors à vérifier que la famille ainis formée
.
Il reste alors à vérifier que la famille ainis formée 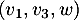 est libre.
est libre.
En effet, si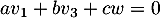 , on a
, on a
![\[\la\begin{array}{rcl}
a+2b+c&=&0\\
-a-b&=&0\\
a+2b&=&0
\enar\right.
\iff\la\begin{array}{rcl}
a+2b+c&=&0\\
-a-b&=&0\\
3b&=&0
\enar\right.\]](/Generateur-Devoirs/Colles/ev/exF1_c/11.png)
d'où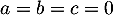 et la famille est libre.
et la famille est libre.
Tag:Espace vectoriel
Autres sujets au hasard:
