Exponentielle et logarithme
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
oral HEC, BL - 2022
- Question de cours : Fonction de répartition et densité d'une variable aléatoire suivant la loi exponentielle de paramètre
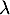 .
.
-
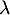 désigne un réel strictement positif. On considère la fonction
désigne un réel strictement positif. On considère la fonction  définie sur
définie sur 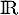 par:
par:
![\[h(x)=\la\begin{array}{cll}\lambda^2xe^{-\lambda x}&\text{si}&x\geqslant0 \\0 &\text{si} &x<0\enar\right.\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1/5.png)
- Montrer que
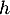 peut être considérée comme la densité de probabilité d'une variable aléatoire
peut être considérée comme la densité de probabilité d'une variable aléatoire 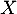 .
.
- Montrer que
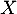 admet une espérance et la calculer.
admet une espérance et la calculer.
- Montrer que
- Dans cette question, on considère une variable aléatoire
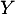 de densité
de densité 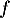 , nulle sur
, nulle sur ![$]-\infty; 0[$](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1/11.png) , continue sur
, continue sur 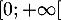 et strictement positive sur
et strictement positive sur  . On note alors
. On note alors 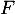 la fonction de répartition de
la fonction de répartition de 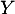 .
.
- Justifier que pour tout réel
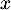 , on a
, on a 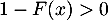 .
.
On définit alors la fonction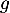 par:
par:
![\[g(x) = \la\begin{array}{cll}-f(x)\ln(1-F(x))&\text{si}&x\geqslant0\\0&\text{si}&x<0\enar\right.\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1/19.png)
- Montrer que
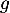 peut être considérée comme la densité d'une variable aléatoire
peut être considérée comme la densité d'une variable aléatoire 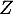 .
.
- Justifier que pour tout réel
Correction
Correction
oral HEC, BL - 2022 - Exercice avec préparation- La densité d'une variable aléatoire
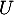 qui suit la loi exponentielle de paramètre
qui suit la loi exponentielle de paramètre 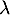 est nulle sur
est nulle sur  et a pour expression
et a pour expression
![\[f_U(x)=\la\begin{array}{cll}\lambda e^{-\lambda x}&\text{pour}&x\geqslant 0\\0&\text{si}&x<0\enar\right.\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/4.png)
La fonction de répartition a quant à elle pour expression
![\[F_U(x)=\la\begin{array}{cll}1-e^{-\lambda x}&\text{pour}&x\geqslant 0\\0&\text{si}&x<0\enar\right.\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/5.png)
-
-
 est une fonction positive, continue par morceaux. Il reste à calculer l'intégrale sur
est une fonction positive, continue par morceaux. Il reste à calculer l'intégrale sur 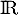 de cette fonction.
de cette fonction.
On peut soit la calculer directement, à l'aide d'une intégration par parties, ou s'aidant de la question précédente, en utilisant l'expérance d'une variable aléatoire suivant la loi exponentielle qui vaut
![\[\begin{array}{ll}E(U)&=\dsp\int_\R xf_U(x)dx\\[1em]
&=\dsp\int_\R\lambda xe^{-\lambda x}dx=\dfrac1\lambda\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/8.png)
On a donc ici,
![\[\int_\R h(x)dx=\lambda\int_R\lambda xe^{-\lambda x}dx=\lambda\tm\dfrac1\lambda=1\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/9.png)
ce qui finit de montrer que est une densité de probabilité.
est une densité de probabilité.
- L'espérance de
 est alors, si elle existe, c'est-à-dire si l'intégrale converge,
est alors, si elle existe, c'est-à-dire si l'intégrale converge,
![\[E(X)=\int_\R xh(x)dx\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/12.png)
On peut là aussi calculer cette intégrale en intégrant par parties, ou utiliser les propriétés de la loi exponentielle, ici sa variance, et la formule König-Huygens:
![\[V(U)=E(Y^2)-E(Y)^2=\dfrac1{\lambda^2}\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/13.png)
d'où
![\[E(Y^2)=\dfrac1{\lambda^2}+E(Y)^2=\dfrac2{\lambda^2}\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/14.png)
et alors
![\[E(X)=\int_\R xh(x)dx=\lambda E(Y^2)=\dfrac2\lambda\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/15.png)
-
-
-
 est une fonction de répartition, et par conséquent
est une fonction de répartition, et par conséquent 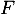 est croissante sur
est croissante sur 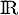 . On a plus précisément
. On a plus précisément  sur
sur 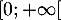 , donc
, donc 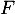 est strictement croissante sur
est strictement croissante sur 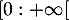 .
.
Comme on sait de plus que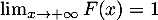 , on a nécessairement que, pour tout réel
, on a nécessairement que, pour tout réel 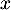 ,
,
![\[F(x)<1\iff 1-F(x)>0\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/25.png)
- D'après ce qui précède, on a que
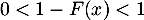 donc
donc
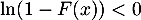 et alors
et alors 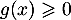 .
.
Comme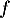 est continue par morceaux, il en va de même pour
est continue par morceaux, il en va de même pour 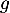 , par produit et composition de fonctions continues par morceaux.
, par produit et composition de fonctions continues par morceaux.
Il nous reste enfin à calculer l'intégrale sur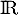 de
de 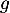 .
.
On a tout d'abord
![\[I=\int_\R g(x)dx=\int_0^{+\infty}-f(x)\ln(1-F(x))dx\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/33.png)
On peut alors intégrer par parties, en se rappelant que :
:
![\[I=\biggl[-F(x)\ln(1-F(x))\biggr]_0^{+\infty}-\int_0^{+\infty}F(x)\dfrac{f(x)}{1-F(x)}dx\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/35.png)
Le terme intégré est nul car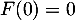 et, par croissances comparées,
et, par croissances comparées,
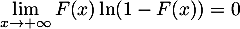 .
.
On a donc
![\[\begin{array}{ll}I&=-\dsp\int_0^{+\infty}\dfrac{F(x)f(x)}{1-F(x)}dx\\
&=\dsp\int_0^{+\infty}\lp\dfrac{1-F(x)}{1-F(x)}f(x)-\dfrac{f(x)}{1-F(x)}\right) dx\\
&=\dsp\int_0^{+\infty}f(x)-\dfrac{F'(x)}{1-F(x)}dx+\\
&=\biggl[F(x) + \ln(1-F(x))\biggr]_0^{+\infty}\\
&=1
\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1_c/38.png)
ce qui finit de démontrer que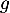 est bien une densité de probabilité.
est bien une densité de probabilité.
-
Tag:Variables aléatoires continues
Autres sujets au hasard:
