Étude et matrice d'une application nilpotente
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
Soit  un endomorphisme de
un endomorphisme de 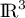 différent de l'endomorphisme nul,
tel que
différent de l'endomorphisme nul,
tel que 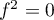 .
.
- Comparer les espaces
 et
et  ,
puis établir leurs dimensions.
,
puis établir leurs dimensions.
- Expliquer pourquoi il existe
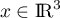 tel que
tel que 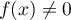 .
.
- Montrer que la famille
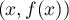 est libre.
est libre.
- En déduire une base telle que la matrice de
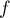 dans cette base soit
dans cette base soit
![\[\lp\begin{array}{ccc}0&1&0\\0&0&0\\0&0&0\enar\rp\]](/Generateur-Devoirs/Colles/Applin/exnil/10.png)
Correction
Correction
- Par définition,
![\[f^2=0\iff\forall x\in\R^3,\ f^2(x)=f\left( f(x)\rp=0\]](/Generateur-Devoirs/Colles/Applin/exnil_c/1.png)
Ainsi, si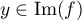 , c'est-à-dire si il
existe
, c'est-à-dire si il
existe  tel que
tel que  , alors on a
, alors on a
![\[f(y)=f(f(x)=f^2(x)=0\]](/Generateur-Devoirs/Colles/Applin/exnil_c/5.png)
ce qui montre que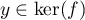 .
.
On a ainsi montré que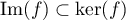 .
.
On en déduit alors que
![\[\text{rg}(f)=\dim\lp\text{Im}(f)\rp\leqslant\dim\lp\ker(f)\rp\]](/Generateur-Devoirs/Colles/Applin/exnil_c/8.png)
On a aussi, par ailleurs, le théorème du rang qui relie ces dimensions:
![\[\text{rg}(f)+\dim\lp\ker(f)\rp=\dim\lp\R^3\rp=3\]](/Generateur-Devoirs/Colles/Applin/exnil_c/9.png)
Comme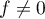 , on a
, on a 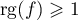 .
Mais on ne peut pas avoir
.
Mais on ne peut pas avoir
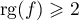 , car alors on aurait
, car alors on aurait
 et donc
et donc
![\[\text{rg}(f)+\dim\lp\ker(f)\rp\geqslant4\]](/Generateur-Devoirs/Colles/Applin/exnil_c/14.png)
ce qui est impossible d'après le théorème du rang.
On a donc nécessairement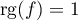 , et alors,
toujours par le théorème du rang,
, et alors,
toujours par le théorème du rang,
 .
.
- Dire que
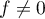 signifie exactement qu'il existe au moins
un élément
signifie exactement qu'il existe au moins
un élément 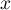 tel que
tel que  .
.
C'est la négation de la définition de l'application nulle:
![\[f=0\iff\Bigl(\forall x\in\R^3, f(x)=0\Bigr)\]](/Generateur-Devoirs/Colles/Applin/exnil_c/20.png)
- Supposons
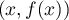 liée, alors
il existe deux réels non nuls
liée, alors
il existe deux réels non nuls 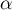 et
et 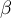 tels que
tels que
![\[\alpha x+\beta f(x)=0
\Longrightarrow x=-\dfrac\beta\alpha f(x)\]](/Generateur-Devoirs/Colles/Applin/exnil_c/24.png)
car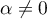 , sinon on aurait
, sinon on aurait 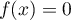 ce qui est contraire à la définiton de
ce qui est contraire à la définiton de  .
On a aurait donc
.
On a aurait donc  , d'où
, d'où
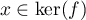 d'après la première question,
c'est-à-dire que
d'après la première question,
c'est-à-dire que 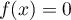 , ce qui est absurde.
, ce qui est absurde.
La famille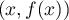 , avec
, avec 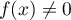 est donc nécessairement libre.
est donc nécessairement libre.
- On a vu que
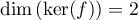 , et d'après ce qui précède,
, et d'après ce qui précède,
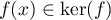 .
.
On complète par un vecteur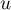 tel que
tel que
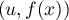 soit une base de
soit une base de 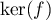 (theorème de la base incomplète),
et on considère enfin la base
(theorème de la base incomplète),
et on considère enfin la base
 .
.
Dans cette base, la matrice de est celle recherchée.
est celle recherchée.
Tag:Applications linéaires
Autres sujets au hasard:

Voir aussi: