Encadrement accroissements finis et convergence d'une somme partielle
Colle de mathématiques
Sujet de colle de maths:- Rolle - AFThéorème de Rolle et théorème des accroissements finis
- SommesSommes des termes d'une suite
Énoncé du sujet
Montrer que pour tout 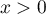 ,
,
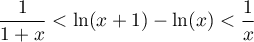 .
.
En déduire, pour tout entier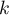 différent de 0 et 1,
la limite lorsque
différent de 0 et 1,
la limite lorsque 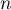 tend vers
tend vers 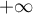 de
de
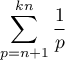 .
.
En déduire, pour tout entier
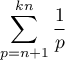 .
.
Correction
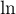 entre
entre 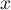 et
et 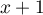 donne l'exsitence d'un réel
donne l'exsitence d'un réel ![$c_x\in]x;x+1[$](/Generateur-Devoirs/Colles/Calcul/exAF4_c/4.png) tel que
tel que
![\[\ln(x+1)-\ln(x)=\ln'\left( c_x\rp=\dfrac{1}{c_x}\]](/Generateur-Devoirs/Colles/Calcul/exAF4_c/5.png)
et donc, comme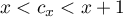 , on a l'encadrement
, on a l'encadrement
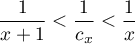 ce qui est bien l'encadrement souhaité.
ce qui est bien l'encadrement souhaité.
On a alors, pour tout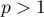 ,
,
![\[\ln(p+1)-\ln(p)<\dfrac1p<\ln(p)-\ln(p-1)\]](/Generateur-Devoirs/Colles/Calcul/exAF4_c/9.png)
et donc, en sommant,
![\[\sum_{p=n+1}^{kn}\ln(p+1)-\ln(p)
<\sum_{p=n+1}^{kn}\dfrac1p<
\sum_{p=n+1}^{kn}\ln(p)-\ln(p-1)
\]](/Generateur-Devoirs/Colles/Calcul/exAF4_c/10.png)
Les sommes qui encadrent sont télescopiques et se simplifient en
![\[\ln(kn+1)-\ln(n+1)
<\sum_{p=n+1}^{kn}\dfrac1p<
\ln(kn)-\ln(n)
\]](/Generateur-Devoirs/Colles/Calcul/exAF4_c/11.png)
soit encore, comme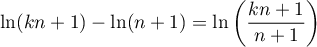 et
et 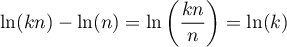 , on a donc
, on a donc
![\[\ln\lp\dfrac{kn+1}{n+1}\right)
<\sum_{p=n+1}^{kn}\dfrac1p<\ln(k)\]](/Generateur-Devoirs/Colles/Calcul/exAF4_c/14.png)
Maintenant, comme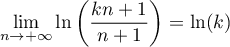 ,
d'après le théorème des gendarmes,
,
d'après le théorème des gendarmes,
![\[\lim_{n\to+\infty}\sum_{p=n+1}^{kn}\dfrac1p=\ln(k)\]](/Generateur-Devoirs/Colles/Calcul/exAF4_c/16.png)
Correction
Le théorème des accroissements finis appliqué à la fonctionet donc, comme
On a alors, pour tout
et donc, en sommant,
![\[\sum_{p=n+1}^{kn}\ln(p+1)-\ln(p)
<\sum_{p=n+1}^{kn}\dfrac1p<
\sum_{p=n+1}^{kn}\ln(p)-\ln(p-1)
\]](/Generateur-Devoirs/Colles/Calcul/exAF4_c/10.png)
Les sommes qui encadrent sont télescopiques et se simplifient en
![\[\ln(kn+1)-\ln(n+1)
<\sum_{p=n+1}^{kn}\dfrac1p<
\ln(kn)-\ln(n)
\]](/Generateur-Devoirs/Colles/Calcul/exAF4_c/11.png)
soit encore, comme
![\[\ln\lp\dfrac{kn+1}{n+1}\right)
<\sum_{p=n+1}^{kn}\dfrac1p<\ln(k)\]](/Generateur-Devoirs/Colles/Calcul/exAF4_c/14.png)
Maintenant, comme
![\[\lim_{n\to+\infty}\sum_{p=n+1}^{kn}\dfrac1p=\ln(k)\]](/Generateur-Devoirs/Colles/Calcul/exAF4_c/16.png)
Tags:Rolle - AFSommes
Autres sujets au hasard:

Voir aussi: