Équation polynomiale de degré 3
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
On considère l'équation 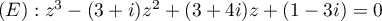
- Vérifier que
 est une racine de
est une racine de 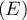 .
.
- Résoudre alors
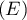 .
.
Correction
 est bien une solution de
est bien une solution de 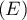 et on trouve alors la factorisation:
et on trouve alors la factorisation:
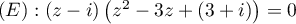 .
.
L'expression du 2nd degré a un discriminant dont on extrait une racine carrée complexe
dont on extrait une racine carrée complexe
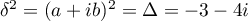 ,
donc
,
donc
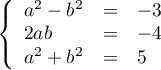 .
.
On trouve ainsi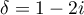 ou
ou  et les deux racines
et les deux racines
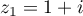 et
et 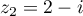 .
.
Correction
L'expression du 2nd degré a un discriminant
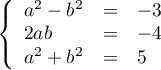 .
.
On trouve ainsi
Tags:ComplexesPolynôme
Autres sujets au hasard:
