Équation différentielle - 1er ordre, coefficients non constants
Colle de mathématiques
Sujet de colle de maths:- Équation différentielleÉquation différentielle
Énoncé du sujet
Résoudre l'équation différentielle
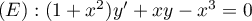
Correction
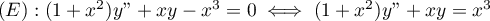
L'équation homogène associée est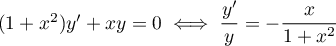
et donc,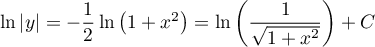
et alors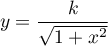 .
.
On peut rechercher une solution particulière polynomiale: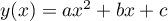 , alors
, alors
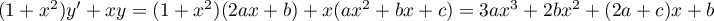
et on doit donc avoir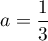 ,
, 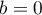 ,
, 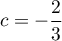 .
.
Une solution particulière est donc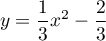 ,
et la solution générale de
,
et la solution générale de 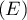 ,
,
![\[y(x)=\dfrac{k}{\sqrt{1+x^2}}+\dfrac13x^2-\dfrac23\]](/Generateur-Devoirs/Colles/EquaDiff/ex5.2_c/12.png)
pour toute constante réelle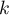 .
.
Correction
L'équation homogène associée est
et donc,
et alors
On peut rechercher une solution particulière polynomiale:
et on doit donc avoir
Une solution particulière est donc
pour toute constante réelle
Tag:Équation différentielle
Autres sujets au hasard:

Voir aussi: