Équation de cercle dans l'espace
Colle de mathématiques
Sujet de colle de maths:- Géométrie dans l'espaceGéométrie dans l'espace
Énoncé du sujet
À tout réel 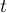 , on associe le point
, on associe le point 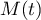 de coordonnées
de coordonnées
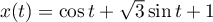 ,
,
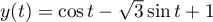 et
et
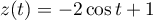 .
.
- Calculer
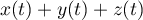 .
.
- Calculer
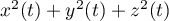 .
.
- En déduire que
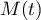 est toujours élément d'un cercle
dont on précisera le centre et le rayon.
est toujours élément d'un cercle
dont on précisera le centre et le rayon.
Correction
Correction
-
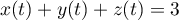 et donc
et donc 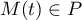 ,
avec
,
avec 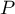 le plan d'équation
le plan d'équation 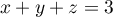 .
.
-
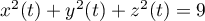 et donc
et donc 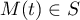 ,
avec
,
avec 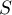 la sphère d'équation
la sphère d'équation 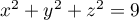 .
.
-
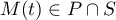 .
Le centre de ce cercle est le projeté orthogonal de
.
Le centre de ce cercle est le projeté orthogonal de 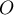 ,
centre de la sphère, sur le plan
,
centre de la sphère, sur le plan 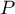 .
On cherche donc
.
On cherche donc 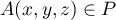 tel que le vecteur
tel que le vecteur 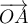 est colinéaire à
est colinéaire à 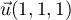 (vecteur normal du plan).
On trouve A(1,1,1).
(vecteur normal du plan).
On trouve A(1,1,1).
Le rayon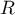 du cercle est, par exemple
du cercle est, par exemple 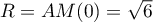 .
.
Tag:Géométrie dans l'espace
Autres sujets au hasard:

Voir aussi: