Ensemble de matrices stable par produit
Colle de mathématiques
Sujet de colle de maths:- MatricesMatrices
Énoncé du sujet
On pose 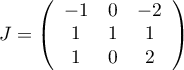 et
et
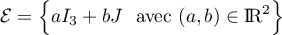 .
.
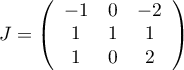 et
et
- Déterminer
 .
.
- Montrer que si
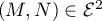 alors
alors
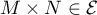 .
.
Correction
Correction
- Le calcul matriciel donne
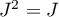 .
.
-
 signifie que
signifie que
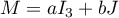 et que
et que
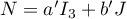 .
.
On a alors,
![\[\begin{array}{ll}M\times N&=\left( aI_3+bJ\rp\times\left( a'I_3+b'J\rp\\
&=aa'I_3+ab'J+ba'J+bb'J^2\enar\]](/Generateur-Devoirs/Colles/matrices/E0_c/5.png)
soit, avec la question précédente
![\[M\times N=aa'I_3+\left( ab'+a'b+bb'\right) J\]](/Generateur-Devoirs/Colles/matrices/E0_c/6.png)
ce qui montre que le produit appartient aussi à
appartient aussi à
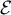 .
.
Tag:Matrices
Autres sujets au hasard:

Voir aussi: