Égalité des noyaux et images de 3 endomorphismes définis par compositions circulaires
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
Soit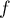 
, 
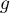et 
trois endomorphismes d'un même espace vectoriel 
tels que
, 
et 
.
Montrer que
, 
et 
ont même noyau et même image.
, et 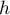trois endomorphismes d'un même espace vectoriel 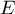tels que
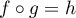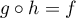, et .
Montrer que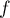
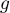, et ont même noyau et même image.
Correction
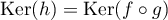et donc, si 
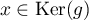c'est-à-dire 
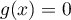donc 
donc 
et ainsi
.
De même, en permuttant circulairement, à partir de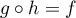
on obtient
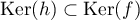et de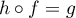 
on tire 
.
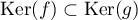Finalement, on a obtenu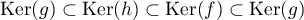
ce qui montre que tous ces noyaux sont égaux.
Concernant les images, soit par exemple
c'est-à-dire qu'il existe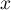 
tel que
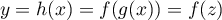avec 
et
donc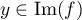 
, d'où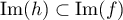 
En permuttant à nouveau circulairemen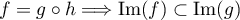t,
et
.
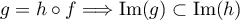Finalement, on a obtenu
![\[\text{Im}(h)\subset\text{Im}(f)\subset\text{Im}(g)\subset\text{Im}(h)\]](/Generateur-Devoirs/Colles/Applin/exAL8_c/20.png)
ce qui montre que toutes ces images sont égales.
Correction
et donc, si c'est-à-dire
donc donc et ainsi
.
De même, en permuttant circulairement, à partir de
on obtient
et de on tire .
Finalement, on a obtenu
ce qui montre que tous ces noyaux sont égaux.
Concernant les images, soit par exemple
c'est-à-dire qu'il existe tel que
avec et
donc , d'où
En permuttant à nouveau circulairement,
et
.
Finalement, on a obtenu
ce qui montre que toutes ces images sont égales.
Tag:Applications linéaires
Autres sujets au hasard:
Voir aussi: