Encadrement suite, intégrale et convergence série
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
On considère, pour  , la série de terme général
, la série de terme général
 .
.
- Donner un encadrement de
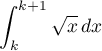 et en déduire un encadrement
de
et en déduire un encadrement
de  .
.
- En déduire un équivalent pour
 puis la nature de la série de terme général
puis la nature de la série de terme général 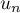 suivant la valeur du paramètre
suivant la valeur du paramètre 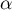 .
.
Correction
Correction
- Comme
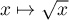 est croissante sur
est croissante sur 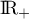 , on a
, on a
![\[\sqrt{k}\leq\int_k^{k+1}\sqrt{x}\,dx\leq\sqrt{k+1}\]](/Generateur-Devoirs/Colles/Series/ssi_c/3.png)
et alors, en sommant ces inégalités pour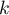 de 1 à
de 1 à 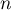 ,
et en utilisant la relation de Chasles pour les intégrales,
on obtient
,
et en utilisant la relation de Chasles pour les intégrales,
on obtient
![\[v_n\leq\int_1^{n+1}\sqrt{x}\,dx\leq v_{n+1}-1\]](/Generateur-Devoirs/Colles/Series/ssi_c/6.png)
L'inégalité de droite s'écrit aussi
![\[\int_1^n\sqrt{x}\,dx\leq v_n-1\]](/Generateur-Devoirs/Colles/Series/ssi_c/7.png)
et on donc l'encadrement
![\[\int_1^n\sqrt{x}\,dx+1\leq v_n\leq\int_1^{n+1}\sqrt{x}\,dx\]](/Generateur-Devoirs/Colles/Series/ssi_c/8.png)
- On calcule alors les intégrales:
![\[\begin{array}{ll}\dsp\int_1^n\sqrt{x}\,dx&=\lb\dfrac23 x^{3/2}\,\rb_1^n\\[1em]
&=\dfrac23\left( n^{3/2}-1\rp\enar\]](/Generateur-Devoirs/Colles/Series/ssi_c/9.png)
et de même pour l'autre intégrale.
On trouve alors que
![\[\dfrac23\left( n^{3/2}-1\rp\leq v_n\leq\dfrac23\left( (n+1)^{3/2}-1\rp\]](/Generateur-Devoirs/Colles/Series/ssi_c/10.png)
et donc l'équivalent
![\[v_n\sim\dfrac23n^{3/2}\]](/Generateur-Devoirs/Colles/Series/ssi_c/11.png)
On a donc
![\[u_n\sim\dfrac23n^{3/2-\alpha}=\dfrac23\,\dfrac1{n^{\alpha-3/2}}\]](/Generateur-Devoirs/Colles/Series/ssi_c/12.png)
puis, par comparaison avec une série de Riemann, on en déduit que la série de terme général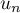 converge si et seulement si
converge si et seulement si
![\[\alpha-\dfrac32>1\iff\alpha>\dfrac52\]](/Generateur-Devoirs/Colles/Series/ssi_c/14.png)
Tags:SériesIntégrale
Autres sujets au hasard:

Voir aussi: